2023년도 겨울학기 과학계산 트레이닝 세션의 네 번째 주제는 저번 주차에서 만든 인지과제를 수행하는 인공신경망의 neural state dynamics 분석 입니다.
이번 주차에는 인공신경망의 neural state dynamics를 분석한 다양한 선행 연구들을 조금씩 소개하고,
선행 연구들의 접근 방법과 의의를 배우고, 우리 문제에 적용해 보겠습니다. 저번 주차에서 우리는 간단한 시각 판별 과제를 구현하고, 이를 수행할 수 있는 RNN 모델을 구현하였습니다.
이후 학습된 RNN 모델을 이용하여 해당 RNN 모델의 행동 데이터와 짧은 꼬리 원숭이의 행동 데이터를 비교해 보았습니다.
하지만 이러한 접근 방법에는 몇 가지 문제점이 존재합니다.
-
첫번째 문제는 우리가 해당 인지과제를 풀기 위해 사용한 신경망 구조가 Biological neural network와 비교하기에 적합하지 않을 수 있다는 것 입니다.
저번 주차에서 우리는 PyTorch에서 제공하는 LSTM 신경망을 사용하였습니다.
하지만 이렇게 구현한 LSTM 신경망은 우리가 해당 신경망에 다양한 제약 조건을 넣어 Biological neural network와 더
유사한 동작을 하게 만드는 데에 여러 어려움이 있습니다. 예를 들어 실제 동물의 뇌에서 관찰되는 조건이 추가된 신경망을 구현하기가 어렵습니다.
-
두번째 문제는 실제 사람이나 동물이 수행하는 인지 과제의 time steps과 RNN의 time steps을 맞추기가 어렵다는 것 입니다.
RNN 모델에 실제 사람이나 동물이 수행하는 인지 과제와 동일한 time steps를 갖는 데이터를 입력하기 위해서
우리는 연속된 데이터를 이산화(discretize) 해야 하는데, 저번 주차에서는 그런 부분이 구현되지 않았습니다.
따라서 이번 주차에는 여러 계산신경과학 선행 연구에서 인지 과제를 수행하는 RNN 모델을 만들기 위해 사용한 방법들을 알아보고,
이를 따라서 구현해 보도록 하겠습니다.
다만 여기서 제가 강조하고 싶은 점은 우리가 RNN 모델을 실제 동물 뇌의 신경망과 유사하게 만들기 위해 하는 방법들에는 명확한 정답이 있기 힘들다는 말씀을 드리고 싶습니다.
이는 저번 주차에서 이야기 한 모델 시스템의 추상화를 어떤 수준에서 할 것인가에 대한 문제이며, 넓게는 자연과학, 좁게는 계산과학이 가지고 있는 근본적인 한계라고 생각 합니다.
모델 시스템을 만들고 이를 분석하며 늘 그런 모델 시스템이 실제 현상과 얼마나 유사한가? 실제 현상을 모델링 하는데 있어서 충분히 유사한가? 와 같은 질문을 얼마든지 던져 볼 수 있습니다.
모든 동료 연구자들이 이건 실제 현상과 완전히 같다고 동의 할 수 있는 수준의 모델 시스템은 없다고 생각 합니다. 만약 그런 연구가 가능하다 하더라도, 그건 모델 시스템을 만들 의미가 없는 연구이기도 하구요.
그래서 우리가 RNN 모델에 어떤 제약 조건을 추가하는 것으로 우리가 실제 뇌의 신경망을 얼마나 잘 모사하고 있는가를 이야기 하기는 어렵다고 생각 합니다.
여기엔 정답은 없고, 다만 선행 연구들이 있을 뿐이죠. 선행 연구들이 설정한 추상화의 수준과 그 모델 시스템을 통해 이야기 할 수 있었던 결론들이
현재 우리 학계가 RNN 모델을 사용한 연구가 신경과학을 연구하는데 있어 유용한 모델 시스템이라고 어느정도 인정하고 있는 수준이다… 정도로 말 할 수 있을것 같습니다.
학습 목표
이번 주차의 학습 목표는 다음과 같습니다.
- 여러 제약 조건이 추가된 RNN 모델을 구현해 봅니다.
- RNN 모델의 neural state dynamics를 분석 합니다.
문제를 정의하기
모든 문제 풀이의 시작은 풀고자 하는 문제를 잘 정의하는 것 입니다. 우리는 위에서 저번 주차에서 구현한 RNN 모델의 두 가지 문제점을 지적하였습니다.
이제 저번 주차에서 RNN 모델을 정의하기 위해 작성한 코드를 보도록 하겠습니다.
class RNN(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
super(RNN, self).__init__()
self.hidden_dim = hidden_dim
self.lstm_layer = nn.LSTM(input_dim, hidden_dim, batch_first=True)
self.fc_layer = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
h0 = torch.zeros(1, x.size(0), self.hidden_dim).to(device)
c0 = torch.zeros(1, x.size(0), self.hidden_dim).to(device)
output, _ = self.lstm_layer(x, (h0, c0))
output = self.fc_layer(output)
return output
위 코드를 보시면 모델에 입력 텐서 x가 들어 올 때 .forward() 메서드가 실행되며 hidden state h와 cell state c를 초기화 한 후,
LSTM 층에 입력 텐서 x가 들어가는 것을 볼 수 있습니다.
이렇게 PyTorch에서 제공하는 LSTM 신경망을 사용하면 우리가 이 신경망을 연구의 목적에 맞게 제약 조건을 걸 수 있는 옵션이 많이 부족합니다.
어떤 RNN 모델을 사용할 것인가? 역시도 수 많은 계산신경과학 논문에서 서로 다 다른 방법을 취하고 있습니다. 저는 최근 저명한 신경과학 저널인 Neuron에 출판된
Guangyu Robert Yang과 Xiao-Jing Wang의 Artificial Neural Networks for Neuroscientists: A Primer 라는 논문을 중심으로
Xiao-Jing Wang 그룹에서 출판된 다양한 논문에서 공통적으로 제시된 방법을 따라서 구현해 보겠습니다.
여러 논문들을 살펴 본 결과 각 논문들이 초점을 맞추고 있는 제약 조건은 조금씩 다르지만 공통적으로 사용하는 몇 가지 제약 조건을 발견하였습니다.
다만 역시 위에서 말씀 드린 대로 모델 시스템을 정의하고 추상화하는데엔 정답이 없고, 연구자에 따라 서로 다른 방법을 사용하고 있다는 점을 꼭 염두해 두셨으면 좋겠습니다.
- RNN 모델의 neural activity를 양수(positive value)로 제한합니다. 이는 실제 동물 뇌의 신경세포의 발화율이 음수로 표현되지 않기 때문입니다.
- RNN 모델의 recurrent unit이 가질 수 있는 neural activity의 크기를 정규화합니다. 이는 RNN 모델이 지나치게 많은 계산 자원을 사용하지 못하도록 제약 조건을 거는 것으로, 실제 동물 뇌의 신경 활동은 에너지를 소모하여 일어나기 때문에 합리적인 제약 조건이라고 말할 수 있겠습니다.
- RNN 모델의 network weight가 희박한(sparse) 연결 구조를 갖게끔 제한합니다. 이는 실제 동물 뇌의 신경세포에서 관찰되는 synaptic connection은 신경세포 사이의 물리적인 거리에 의한 제약 조건이 존재하고, 따라서 fully-connected 되어있지 않기 때문입니다. 포유류의 대뇌 피질에서 관찰되는 synaptic connection의 비율은 약 12% 라는 선행 연구가 존재하고, 우리는 이 비율에 근사하도록 인공신경망에게 제약 조건을 걸 수 있습니다.
이외에도 여러 전기생리학 연구에서 측정된 대뇌 피질의 신경 세포의 특징에 기반한 다양한 제약 조건을 생각 해 볼 수 있겠습니다.
그리고 그런 제약 조건 하에서 정의된 인공신경망 모델의 state dynamics와 행동 데이터가 어떻게 실제 뇌의 neuronal dynamics와 mental state를 더 잘 반영하는 모델 시스템인지 연구하는 것도 계산신경과학의 주요한 연구 방향이 아닐까 싶습니다.
이제 위 세 가지 제약 조건을 건 Continous-time RNN(CTRNN) 모델을 구현해 보겠습니다.
먼저 RNN 모델의 single-unit의 recurrent neural activity $\mathbf{r}(t)$을 시간에 대한 미분방정식으로 표현하면 다음과 같습니다.
\[\tau \frac{d\mathbf{r}}{dt} = -\mathbf{r}(t) + f(W_r \mathbf{r}(t) + W_x \mathbf{x}(t) + \mathbf{b}_r)\]
위 미분방정식은 신경망의 recurrent neural activity인 $\mathbf{r}(t)$가 시간에 따라 어떻게 변화하는지 나타냅니다.
먼저 시간에 따라 신경망에 입력되는 input sequence $\mathbf{x}(t)$는 신경망의 recurrent neural activity $\mathbf{r}(t)$와 가중합(weighted sum) 되고,
이는 신경망이 정보를 비선형 변환하기 위해 고안된 활성화 함수(activation function)인 $f(\cdot)$을 거치게 됩니다. 사용되는 활성화 함수 $f(\cdot)$의 종류에 대해서는 이후에 논의해 보도록 하겠습니다.
$ -\mathbf{r}(t) $ 항의 경우 미분방정식에서 Leaky integration이라 불리는 항으로 이전 neural activity $\mathbf{r}(t)$에 비례하여 다음 neural activity의 크기를 감소시키는 역할을 합니다.
해당 항이 없는 경우 신경망의 상태가 시간에 따라 무한히 증가하여 불안정한 네트워크 상태를 가지게 됩니다. 이제 이 미분방정식을 Euler method를 이용하여 이산화 합니다.
이 부분을 구현하기 위하여 위 논문과 Guangyu Robert Yang의 튜토리얼을 참고하였습니다.
\[\begin{aligned}
\mathbf{r}(t+\Delta t) \approx \mathbf{r}(t) + \Delta \mathbf{r} &= \mathbf{r}(t) + \frac{\Delta t}{\tau}[-\mathbf{r}(t) + f(W_r \mathbf{r}(t) + W_x \mathbf{x}(t) + \mathbf{b}_r)] \\
&= (1 - \frac{\Delta t}{\tau})\mathbf{r}(t) + \frac{\Delta t}{\tau}f(W_r \mathbf{r}(t) + W_x \mathbf{x}(t) + \mathbf{b}_r)
\end{aligned}\]
RNN 모델의 구현과 학습
이제 이렇게 이산화 된 RNN 모델을 PyTorch를 이용하여 구현해 보겠습니다.
RNN 모델의 neural activity를 positive value로 제한한다는 1번 제약 조건을 걸기 위해 모델에서 사용되는 활성화 함수 $f(\cdot)$는
렐루 함수(Rectified Linear Unit, ReLU)를 사용해 보도록 하겠습니다.
class RNN(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim, dt):
super().__init__()
self.input_dim = input_dim
self.hidden_dim = hidden_dim
self.output_dim = output_dim
self.dt = dt
self.tau = 100
self.i2h = nn.Linear(input_dim, hidden_dim)
self.h2h = nn.Linear(hidden_dim, hidden_dim)
self.h2o = nn.Linear(hidden_dim, output_dim)
def forward(self, x):
hidden = torch.zeros(x.size(0), x.size(1), self.hidden_dim)
output = torch.zeros(x.size(0), x.size(1), self.output_dim)
h = torch.zeros(x.size(0), self.hidden_dim).to(device)
for t in range(x.size(1)):
h = h * (1 - self.dt/self.tau) + (self.dt/self.tau) * torch.relu(self.i2h(x[:,t,:]) + self.h2h(h))
o = self.h2o(h)
hidden[:,t,:] = h
output[:,t,:] = o
return output, hidden
위 코드를 보시면 입력 텐서를 hidden layer로 넘겨주는 Linear transformation .i2h()와
시간 $t$에서의 hidden state 텐서를 시간 $t+1$에서의 hidden state 텐서로 변환하는 .h2h(),
마지막으로 hidden state 텐서를 출력 텐서로 변환하기 위한 .h2o() 선형 변환을 정의해 주었습니다.
이후 모델이 실제로 정보를 다음 time step으로 넘겨주는 recurrent neural activity는
위 미분방정식을 오일러법으로 근사한 수식을 .forward() 메서드에 직접 구현해 주었습니다.
위 수식에서 시간 상수 $\tau$는 선행 연구에 따라 100ms로 설정하였고,
$\mathbf{b}_r$항의 경우 선형 변환에 이미 포함 되어 있기 때문에 따로 구현해 줄 필요가 없습니다.
이제 마찬가지로 RNN 모델의 학습과 테스트에 사용되는 시각 판별 과제를 생성하는 VisualDiscrimination() 클래스를 수정하여
미소 시간 변수 .dt에 따라 다운샘플링을 하도록 수정합니다. 대부분 저번 주차에서 했던 코드와 크게 다르지 않으며 샘플링 구간을 나타내는 변수 .dt 만 추가가 되었습니다.
class VisualDiscrimination(Dataset):
def __init__(self, task_dict):
self.target_dim = task_dict['target_dim'] # Red and Green
self.color_dim = task_dict['color_dim']
self.output_dim = task_dict['output_dim'] # Left and Right
self.dt = task_dict['dt']
self.target_onset_range = task_dict['target_onset_range']
self.decision_onset_range = task_dict['decision_onset_range']
self.coherence_range = task_dict['coherence_range']
self.trial_length = task_dict['trial_length']
assert np.max(self.decision_onset_range) < self.trial_length
self.trial_steps = int(self.trial_length/self.dt)
def __getitem__(self, idx):
target_onset = int(np.random.randint(self.target_onset_range[0], self.target_onset_range[1])/self.dt)
decision_onset = int(np.random.randint(self.decision_onset_range[0], self.decision_onset_range[1])/self.dt)
coherence = np.random.uniform(low=self.coherence_range[0], high=self.coherence_range[1])
input_seq = np.zeros((self.trial_steps, self.target_dim+self.color_dim))
output_seq = np.zeros((self.trial_steps, self.output_dim))
checkerboard_color = np.sign(np.random.normal()) # -1(Red) or +1(Green)
target_idx = np.random.randint(0, self.output_dim) # 0(Red-Green) or 1(Green-Red)
# Target cue
input_seq[target_onset:, target_idx] = 1
# Color checkerboard
input_seq[:, self.target_dim:] = np.random.normal(loc=0, size=(self.trial_steps, self.color_dim))
input_seq[decision_onset:, self.target_dim:] = np.random.normal(loc=checkerboard_color*coherence,
size=(self.trial_steps-decision_onset, self.color_dim))
# Desired output
color_idx = 1 if checkerboard_color > 0 else 0 # (0: Red, 1: Green)
output_direction = 0 if color_idx == target_idx else 1 # (0: Left, 1: Right)
output_seq[decision_onset:, output_direction] = 1
return {'input_seq': input_seq, 'output_seq': output_seq,
'checkerboard_color': checkerboard_color, 'coherence': coherence,
'target_idx': target_idx, 'output_direction': output_direction, 'decision_onset': decision_onset}
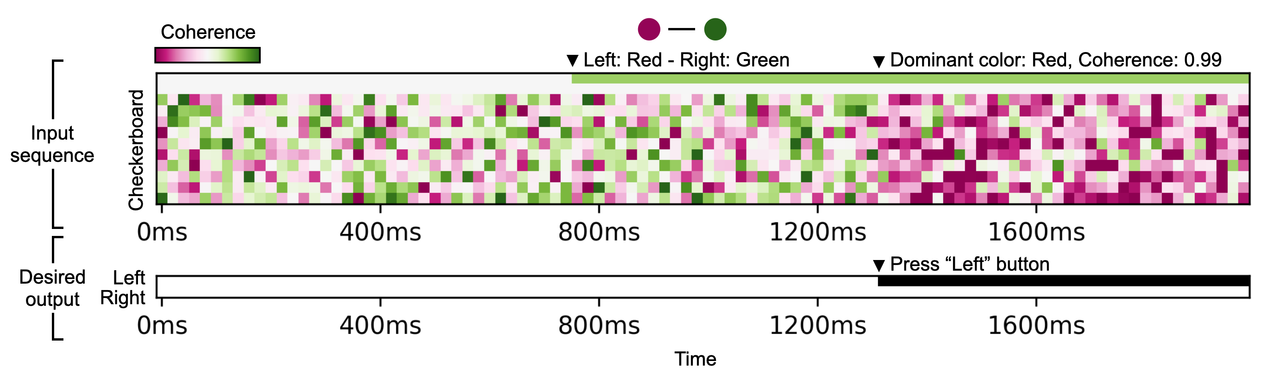 Figure 1. 시각 판별 과제의 예시
Figure 1. 시각 판별 과제의 예시
이제 2번과 3번 제약 조건을 추가하여 RNN 학습을 진행합니다. 2번 제약 조건은 RNN 모델의 recurrent unit의 활성화, 즉 firing rate를 정규화 하는 것이고,
3번 제약 조건은 RNN 모델의 weight를 희소하게 만드는 것 입니다. 우리는 L1 정규화(regularization)를 통해 RNN 모델에 2번과 3번 제약 조건을 걸 수 있습니다.
\[\begin{aligned} L_{\text{L1, rate}} &= \beta_{\text{rate}} \sum_{i,t} \lvert \mathbf{r_{i,t}} \rvert \\ L_{\text{L1, weight}} &= \beta_{\text{weight}} \sum_{l} \sum_{i,j} \lvert \mathbf{w_{i,j}^{l}} \rvert \end{aligned}\]
우리는 신경망의 트레이닝 스텝에서 rate와 weight를 정규화하기 위한 loss를 구한 후, 이를 신경망의 오차 함수에 더해주면 됩니다.
최종 loss에 단순히 더하기만 하면 학습이 된다는 점이 무척 신기할 수 있으나, 이는 PyTorch의 강력한 자동 미분(autograd) 기능을 통해
각 오차를 손쉽게 신경망으로 역전파 할 수 있기 때문입니다.
task_params = {'target_dim': 2,
'color_dim': 10,
'output_dim': 2,
'dt': 20,
'target_onset_range': (400, 900),
'decision_onset_range': (1200, 1800),
'trial_length': 2000,
'coherence_range': (0.0, 1.0)}
input_dim = task_params['target_dim']+task_params['color_dim']
trial_steps = int(task_params['trial_length']/ task_params['dt'])
hidden_dim = 128
output_dim = task_params['output_dim']
dt = task_params['dt']
batch_size = 128
num_epochs = 4000
learning_rate = 0.001
beta_rate = 10e-7
beta_weight = 10e-5
model = RNN(input_dim, hidden_dim, output_dim, dt).to(device)
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=learning_rate)
loss_history = []
L1_rate_history = []
L1_weight_history = []
dataset = VisualDiscrimination(task_params)
for epoch in range(num_epochs):
inputs = torch.zeros((batch_size, trial_steps, input_dim))
targets = torch.zeros((batch_size, trial_steps, output_dim))
for i in range(batch_size):
data = dataset[0]
inputs[i], targets[i] = torch.tensor(data['input_seq']), torch.tensor(data['output_seq'])
inputs.to(device)
targets.to(device)
optimizer.zero_grad()
outputs, hidden_state = model(inputs)
loss = criterion(outputs, targets)
L1_rate = beta_rate * torch.norm(hidden_state, 1)
model_weight = torch.cat([x.view(-1) for x in model.parameters()])
L1_weight = beta_weight * torch.norm(model_weight, 1)
total_loss = loss + L1_rate + L1_weight
total_loss.backward()
optimizer.step()
loss_history.append(loss.item())
L1_rate_history.append(L1_rate.item())
L1_weight_history.append(L1_weight.item())
if epoch % 100 == 0:
print (f'Training epoch ({epoch+1}/{num_epochs}), Total loss: {total_loss.item():3.3f}, '
f'loss: {loss.item():3.3f}, L1 norm(rate): {L1_rate:3.3f}, L1 norm(weight): {L1_weight:3.3f}')
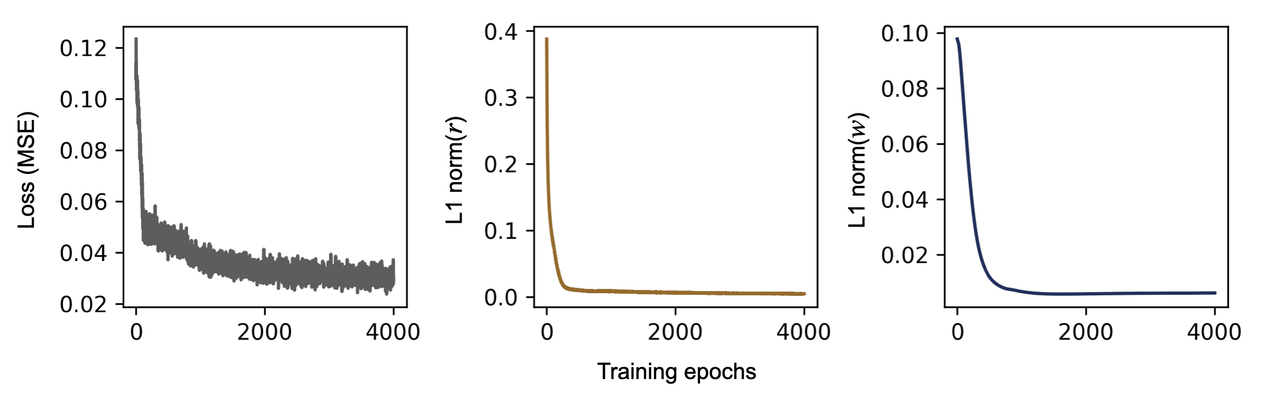 Figure 2. 제약 조건이 추가된 RNN 모델의 학습 곡선
Figure 2. 제약 조건이 추가된 RNN 모델의 학습 곡선
학습을 통해 모델의 세 loss가 충분히 잘 줄어든 것을 확인 할 수 있습니다.
모델은 2번과 3번 조건을 만족하기 위해 매우 효율적인 recurrent connection을 구축하게 됩니다.
우리가 정의한 문제의 경우 그렇게 복잡하지 않아 어떤 제약조건 하에서라도 모델은 쉽게 문제를 풀 수 있지만,
만약 RNN 모델이 여러 인지 과제를 동시에 수행해야 하는 경우 이러한 기법을 통해 더 효율적인 구조를 갖추는 것이 성능에 영향을 주게 됩니다.
 Figure 3. Weight의 L1 정규화의 유무에 의한 RNN 모델의 network weight matrix 비교
Figure 3. Weight의 L1 정규화의 유무에 의한 RNN 모델의 network weight matrix 비교
그림 3에서 볼 수 있듯 똑같은 과제를 수행하는 두 RNN 모델의 network weight가 어떻게 구성되었는지 확인 할 수 있습니다.
network weight의 L1 정규화가 적용된 RNN 모델(오른쪽)은 매우 희소한 network connection을 가지고 있음을 볼 수 있습니다. 저 많은 neuron 중에 일 하는 neuron의 수는 극소수군요…
물론 희소한 network connection을 RNN 모델(오른쪽)이 살짝 더 낮은 model performance를 보이나, 큰 차이라고 볼 수 없고,
connection의 개수 대비 model performance는 훨씬 더 뛰어나기 때문에 효율적인 연결 구조를 가지게 되었다고 말 할 수 있겠습니다.
RNN 모델의 state dynamics 분석
이제 학습된 RNN 모델의 recurrent neural activity $\mathbf{r}(t)$이 인지 과제를 수행하는 동안 어떤 dynamics를 가지고 있는지 살펴보겠습니다.
먼저 쉽게 해 볼 수 있는 분석은 시각 판별 과제의 조건에 따라 RNN 모델의 neural trajectory가 어떤지 확인하는 것 입니다.
먼저 VisualDiscrimination() 클래스를 이용하여 테스트 데이터를 생성 시킨 후, neural trajectory를 주성분분석(PCA)을 통해 3개의 차원으로 축소해 보았습니다.
너무 길어져서 아래 코드에는 따로 나타내지 않았지만, 사실 task_params_test 딕셔너리를 조절하며 다음과 같은 분석 절차를 거쳤습니다.
- RNN 모델의 학습에 사용된 것과 같은 과제 조건을 이용하여 데이터를 생성 시킨 후, 이를 이용하여 PCA 모델을 학습합니다. (
pca_mode.fit(X))
- 시간에 따라 변화하는 neural state(trajectory)의 분석을 용이하게 하기 위해 시간
task_params_test 딕셔너리를 조절하여 target_onset을 800ms, decision_onset을 1600ms로 고정한 시행을 생성합니다.
- 이때 2번에서 생성하는 시행의 경우 color coherence가 (0.95, 1.0) 사이인 High color coherence 조건과 color coherence가 (0.0, 0.05) 구간에서 샘플링 되는 Low color coherence 조건을 나누었습니다.
- 조건별 시행을 1에서 학습 된 PCA 모델로 차원을 축소하여 저차원 공간에 임베딩 합니다. (
pca_model.transform(X))
from sklearn.decomposition import PCA
test_batch_size = 512
dataset = VisualDiscrimination(task_params_test)
with torch.no_grad():
inputs = torch.zeros((test_batch_size, trial_steps, input_dim))
targets = torch.zeros((test_batch_size, trial_steps, output_dim))
coherence = np.zeros(test_batch_size)
color = np.zeros(test_batch_size)
desired_direction = np.zeros(test_batch_size)
decision_onset = np.zeros(test_batch_size)
for i in range(test_batch_size):
data = dataset[0]
inputs[i], targets[i] = torch.tensor(data['input_seq']), torch.tensor(data['output_seq'])
color[i], coherence[i] = data['checkerboard_color'], data['coherence']
desired_direction[i], decision_onset[i] = data['output_direction'], data['decision_onset']
inputs.to(device)
outputs, hidden_state = model(inputs)
outputs = outputs.cpu().numpy()
hidden_state = hidden_state.cpu().numpy()
targets = targets.cpu().numpy()
pca_model = PCA(n_components=3)
pca_model.fit(hidden_state.reshape(-1,hidden_dim))
reduced_hidden_state = np.zeros((test_batch_size, trial_steps, 3))
for i in range(test_batch_size):
reduced_hidden_state[i] = pca_model.transform(hidden_state[i])
PCA 분석을 통해 저차원에 임베딩한 RNN model의 neural trajectory는 다음과 같습니다.
우리가 사용한 시각 판별 과제는 과제 시작 후 800ms에서 타겟 정보가 주어집니다.
해당 타겟 정보는 빨간색이 왼쪽인지(이 경우에 초록색은 오른쪽 입니다), 혹은 오른쪽인지(이 경우엔 초록색은 왼쪽 입니다) 알려주는 시각 단서를 포함하고 있습니다.
이후 1600ms에서 주어지는 checkerboard의 색에 따라 RNN 모델은 왼쪽 혹은 오른쪽을 응답하게 됩니다.
만약 타겟 정보가 빨간색이 왼쪽이고(즉 초록색은 오른쪽) 제시되는 checkerboard의 색이 빨간색인 경우 RNN 모델은 왼쪽을 응답하면 됩니다.
1600ms에서 주어지는 checkerboard는 색을 판별하는 것은 각 시행의 color coherence 값에 따라 난이도가 달라지게 됩니다.
 Figure 4. color coherence에 따른 RNN 모델의 neural trajectory
Figure 4. color coherence에 따른 RNN 모델의 neural trajectory
RNN 모델의 neural trajectory를 보면 color coherence가 높은 시행에서 각각의 조건과 분기에 맞추어 neural state가 선명하게 나누어 지는 것을 볼 수 있습니다.
즉 모델은 800ms에서 해당 시행의 타겟 정보에 따라 state가 분리되고 이어서 1600ms에서 checkerboard의 색 정보가 주어질 때 서로 다른 response를 낼 수 있는 형태로
state가 나누어 지는 것을 볼 수 있습니다. 반면 color coherence가 낮은 시행의 경우 모델은 주어지는 타겟 정보에 따라 state를 분리하였으나
checkerboard의 color를 제대로 식별하지 못해 state가 잘 나누어 지지 않는 모습을 확인 할 수 있습니다.
이렇게 저차원에서 neural trajectory를 그려서 직관적으로 모델의 state dynamics를 확인해 볼 수 있었습니다.
하지만 이러한 neural state dynamics를 어떻게 더 정량적으로 분석 할 수 있을까요?
예를 들어서 위에서 우리가 neural trajectory를 보고 직관적으로 알 수 있었던 “state가 4개로 분리 되는 것”은 dynamical system에서 어떤 의미일까요?
RNN 모델에서 state의 변화는 비선형적으로 동작하며, 이러한 비선형 동역학 시스템에서는 시간과 차원을 따라 정보의 흐름을 추적하고, 해석하기 대단히 어렵습니다.
이러한 RNN 모델의 state dynamics를 해석 하기 위한 방법으로 많은 선행연구에서는 Fixed point를 이용합니다 (Sussillo and Barak, 2013).
동역학 시스템에서 fixed point는 시간에 따른 state dynamics가 수렴할 수 있는 안정적인 상태를 말합니다 (repeller와 같은 unstable fixed point도 있으나, 이는 일단 이야기 하지 않겠습니다).
이러한 fixed point 근처에서 네트워크의 state dynamics는 그 변화의 크기가 크지 않아 이를 선형 동역학 시스템으로 근사 할 수 있습니다.
우리가 비선형 시스템을 선형 시스템으로 근사하게 되면 시스템의 변화를 쉽게 예측 할 수 있고, 또한 이를 각 요소로 분해하여 해석 할 수 있습니다.
이제 우리가 학습 시킨 RNN 모델에서 안정적인 상태를 갖는 fixed point를 찾는 방법을 알아 보겠습니다. 먼저 시간에 따른 state의 변화의 정도를 각 state에 대한 함수 $\mathbf{F}(\mathbf{r})$로 나타 낼 수 있습니다.
\[\frac{d\mathbf{r}}{dt} = \mathbf{F}(\mathbf{r})\]
시간 $t$에서 neural state $\mathbf{r}$는 상태 공간(state space)의 한 점으로 생각 할 수 있습니다.
그 점은 다음 time step인 $t+1$에서 새로운 점(새로운 상태)으로 이동합니다. 즉 함수 $\mathbf{F}(\mathbf{r})$의 의미는 state $\mathbf{r}$을 시간으로 미분한, 즉 그 상태의 이동 속도라고 생각 할 수 있습니다.
Fixed point는 이러한 상태의 이동 속도 $\mathbf{F}(\mathbf{r})$가 0이 되는 시점이라 생각 할 수 있습니다.
이러한 Fixed point $\mathbf{r}_F$ 근방의 state인 $\mathbf{r}_F + \Delta \mathbf{r}$의 dynamics는 다음과 같이 선형 근사가 가능합니다.
\[\mathbf{F}(\mathbf{r}) = \mathbf{F}(\mathbf{r}_F + \Delta \mathbf{r}) \approx \mathbf{F}(\mathbf{r}_F) + \mathbf{J}(\mathbf{r}_F)\Delta \mathbf{r}\]
$\mathbf{J}$는 함수 $\mathbf{F}$의 Jacobian matrix로 함수 $\mathbf{F}$의 1차 편미분 계수로 구성되어 있습니다. 이의 기하학적 의미 역시도 미소 영역에서 비선형 변환의 선형 근사를 의미합니다.
혹시 이에 대해 더 궁금하다면 관련 학습 자료를 추천합니다.
그럼 이제 fixed point에서 우리는 RNN의 비선형 동역학을 선형 근사 할 수 있음을 알았으니 $\mathbf{F}(\mathbf{r}) = 0$인 $\mathbf{r}_F$를 찾아보면 되겠습니다.
이를 손으로 풀어서 analytic solution을 얻을 수 있으면 좋겠으나, 신경망을 이용한 시스템이 대부분 그러하듯 우리는 $\mathbf{F}(\mathbf{r}) = 0$인 analytic solution을 찾을 수 없을 것입니다.
다시 말해 $\mathbf{F}(\mathbf{r})$가 최소가 되는 상태 $\mathbf{r}$을 수치 해석과 최적화를 이용해 찾아야 하는 것입니다.
\[\mathrm{argmin}_{\mathbf{r}} |F(\mathbf{r})|^2\]
그럼 이건 또 어떻게 찾을 수 있을까요(ㅋㅋ)? 여기엔 여러 방법이 있겠습니다만, 결국 수치 해석과 최적화가 하는 일은 다 똑같습니다…
목표 함수를 정의하고, 목표 함수를 최소(혹은 최대)로 하는 최적화를 수행 합니다. 저는 PyTorch의 자동 미분을 이용하여 경사 하강법(gradient descent)을 사용해 보겠습니다.
목표 함수는 RNN 모델의 hidden state h와 다음 time step에서의 state인 h_new 사이의 크기인 h_diff가 최소가 되는 방향으로 h의 그래디언트를 계산하여 하강(?)해 줍니다.
이때 RNN 모델의 hidden state h는 시작 값을 임의의 값으로 초기화하여 넓은 상태 공간(state space)를 탐색해 보도록 하겠습니다.
from torch.autograd import Variable
def sample_const_input(target_idx = 0, checkerboard_color = +1, coherence = 0.95):
const_input = np.zeros((1, 1, task_params['target_dim']+task_params['color_dim']))
const_input[0, 0, target_idx] = 1
const_input[0, 0, task_params['target_dim']:] = np.random.normal(loc=checkerboard_color*coherence, size=(1, task_params['color_dim']))
return torch.tensor(const_input).to(device)
def find_fixed_point(model, x, h):
gamma = 0.05
count = 0
while True:
h = Variable(h).to(device)
h.requires_grad = True
h_new = h * (1 - model.dt/model.tau) + (model.dt/model.tau) * torch.relu(model.i2h(x[0,0,:]) + model.h2h(h))
h_diff = torch.norm(h - h_new)
h_diff.backward()
if h_diff.item() < 10e-4:
return h, True
gamma *= (1-10e-5)
h = h - gamma * h.grad
count += 1
if count == 100000:
print(f'Cannot find fixed point! h_diff={h_diff}')
return h, False
fixed_points = []
for target_idx in [0, 1]:
for checkerboard_color in [-1, 1]:
print("condition:", target_idx, checkerboard_color)
fixed_points.append([])
for i in range(5):
const_input = sample_const_input(target_idx, checkerboard_color).float()
hidden_random = torch.randn(hidden_dim).float()
fixed_point, is_fixed = find_fixed_point(model, const_input, hidden_random)
if is_fixed:
fixed_points[-1].append(fixed_point.detach().cpu().numpy())
 Figure 5. Vector field of the state dynamics (왼쪽), Fixed point의 위치와 state trajectory (오른쪽)
Figure 5. Vector field of the state dynamics (왼쪽), Fixed point의 위치와 state trajectory (오른쪽)
State transition의 방향을 나타내는 vector field와 state trajectory를 저차원에 그리기 위해 위에서 학습한 PCA 모델을 이용하였습니다.
먼저 네 조건(두 개의 타겟 조건과 두 개의 색 조건, color coherence는 모두 0.95로 설정)이 각각
어떤 state로 수렴하는지 확인하기 위해 state transition을 vector field로 나타내 보았습니다.
그림 5의 왼쪽 vector field를 보면 각 조건에 해당하는 자극이 주어질 때 네트워크의 상태가 대략 4개의 클러스터로 수렴하는 양상을 볼 수 있습니다.
Left(Green) - Right(Red) 타겟에서 빨간색 checkerboard가 주어 질 때의 시행에서 최종적으로 상태가 수렴 되는 fixed points를 오른쪽 그림에 나타내었습니다.
이처럼 RNN 모델을 dynamical system으로 해석하여 실제로 상태 공간 상에서 일어나는 state dynamics를 정량적으로 분석 해 볼 수 있었습니다.
ㅎㅎ 사실 여기까지는 정말 기초적인 dynamical system에 대한 분석이고, 여러분들은 여러 참고 문헌을 통해
계산된 jacobian matrix $\mathbf{J}$을 분석하며 더 재미있는 결론을 찾아 볼 수 있을 것입니다. 이는 여러분에게 맡기도록 하겠습니다.
마치며
또 뭐 글을 거의 2주를 넘게 썼네요. 평소에 공부해 보면 좋을 것 같다고 생각한 주제였는데,
또 막상 해보니 이런 접근 방법의 문제점을 금방 알 것 같기도 합니다.
생각보다 RNN 모델의 dynamics를 분석 하는 것이 (여러 선행 연구의 예제만큼) 쉽고 간단하지는 않네요.
의외로 잘 수렴하지 않는 부분도 있고… 문제가 너무 간단해서인지 RNN 모델이 넓은 state space를 충분히 잘 활용하지 못한다는 느낌을 받았습니다.
그리고 제가 진짜로 하고 싶은 state dynamics 연구에 이런 계산 모델과 분석 기법을 어떻게 적용 할 수 있을지 심도 있는 고민을 해 본 시간이었습니다.
오늘은 수식이 참 많았습니다. 제가 이런 연구 주제를 볼 때마다 늘 하는 생각인데… 저는 사실 수식 보다는 실제 구현이 더 중요하다는 생각이 듭니다.
많은 선행 연구들이나 참고 문헌 등에서도 논문에 적힌 수식이 어떻게 실제 구현으로 이어지는지 잘 설명해 주지는 않는 것 같더라구요.
특히 인공신경망을 이용한 계산신경과학 연구에서는 명쾌한 analytic solution을 구하지 못하고, 결국 수치해석과 최적화를 이용한 근사인데,
풀지도 못하는, 게다가 대부분의 파라미터가 신경망으로 대체되는 방정식만 설명을 하는 것은 무슨 의미인가… 싶은 생각도 드네요.
그래서 최대한 수식과 함께 실제 구현에 대해서 잘 설명 드리려고 생각 하고 있습니다. 물론 관련 분야의 연구자로서 수식을 통한 표현도 잘 알고 있으려고 노력하고 있습니다.
아무튼 제 바람은 이 글을 보시는 여러분들이 수식과 함께 이를 실제로 코드를 통해 어떻게 구현하는지를 더 깊게 생각해 보셨으면 좋겠습니다.
다음 시간에는 더 재미가 있는 주제로 찾아뵙도록 하겠습니다. 읽어주셔서 감사합니다.
Recommended reading
- Chandrasekaran, C., Peixoto, D., Newsome, W. T. & Shenoy, K. V. Laminar differences in decision-related neural activity in dorsal premotor cortex. Nat Commun 8, 614 (2017).
- Yang, G. R. & Wang, X.-J. Artificial Neural Networks for Neuroscientists: A Primer. Neuron 107, 1048–1070 (2020).
- Yang, G. R., Joglekar, M. R., Song, H. F., Newsome, W. T. & Wang, X.-J. Task representations in neural networks trained to perform many cognitive tasks. Nat Neurosci 22, 297–306 (2019).
- Chaisangmongkon, W., Swaminathan, S. K., Freedman, D. J. & Wang, X.-J. Computing by Robust Transience: How the Fronto-Parietal Network Performs Sequential, Category-Based Decisions. Neuron 93, 1504-1517.e4 (2017).
- Sussillo, D. & Barak, O. Opening the Black Box: Low-Dimensional Dynamics in High-Dimensional Recurrent Neural Networks. Neural Comput 25, 626–649 (2013).
- Mante, V., Sussillo, D., Shenoy, K. V. & Newsome, W. T. Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 503, 78–84 (2013).
- Goudar, V. & Buonomano, D. V. Encoding sensory and motor patterns as time-invariant trajectories in recurrent neural networks. Elife 7, e31134 (2018).