레이트레이싱과 컴퓨터 그래픽스

January 08, 2023

2023년도 겨울학기 과학계산 트레이닝 세션의 두번째 주제는 컴퓨터를 이용해 빛을 추적하여 장면을 렌더링하는 기법인 Ray tracing 입니다. 이번 주제는 첫 주차 주제보다 수학적인 요소도 많고, 이를 컴퓨터를 이용하여 구현하는 것도 조금 더 어려운데요. 대신 그만큼 더 재미있고 배우는 것이 많은 주제라고 생각합니다. 이번 주차를 수행하며 여러분은 실제로 현대 컴퓨터 그래픽스에서 널리 쓰이는 렌더링 방법중 하나인 레이트레이싱을 파이썬을 이용해 직접 구현하게 됩니다. 이를 구현하는 과정에서 여러분은 공간 벡터의 개념과 구현 및 응용 그리고 객체지향 프로그래밍을 연습 할 수 있습니다. 과제 수행에 필요한 모든 소스 코드는 설명과 함께 주어지지만, 전체 소스 코드가 제공되지 않기 때문에 여러분들은 주어진 설명을 이해하고, 논리 흐름에 맞게 전체 소스 코드를 완성하셔야 합니다. 마지막으로 과제 페이지 끝에 도전자들을 위한 도전 문제가 주어지나, 필수 제출 과제는 아닙니다. 도전 문제는 꽤 어렵지만 도전해 보신다면 과학계산 프로그래밍 연습에 많은 도움이 될 것이라 생각합니다.

학습 목표

이번 주차의 학습 목표는 다음과 같습니다.

• 컴퓨터 그래픽 렌더링 기법인 레이트레이싱의 개념을 이해합니다.
• 빛과 다양한 객체를 공간 벡터를 이용하여 수학적으로 정의합니다.
• 프로그래밍을 통해 빛의 반사와 물체의 색 표현을 구현합니다.

또한 공식적인 학습 목표는 아니지만 이번 주차의 학습을 진행하며 여러분들은 공간, 벡터 등 다양한 개념들의 수학적 정의(수식 등)와 이를 구현하기 위한 프로그래밍 코드 사이의 관계에 조금더 익숙해지실 거라고 기대하고 있습니다.

레이트레이싱을 이용한 렌더링

우리가 시각 시스템을 통해 물체를 볼 수 있는 원리는 무엇일까요? 많은 분들이 답을 잘 알고 계시겠지만 우리는 눈으로 들어오는 빛, 즉 광선을 통해서 물체를 볼 수 있습니다. 태양, 전구 등 광원(Light source)에서 나온 빛이 물체에 반사되고, 물체가 가진 물리적인 특성에 따라 광선의 파장이 바뀌고, 바뀐 광선의 파장을 통해 우리는 물체를 볼 수 있습니다.

레이트레이싱, 우리말로 광선추적 기법은 컴퓨터 그래픽의 렌더링 기법중 하나로, 우리가 빛을 통해 물체를 볼 수 있는 원리를 컴퓨터를 이용해 직관적으로 구현하는 기법입니다. 실제로 다른 점이 있다면 광원에서 나온 빛을 추적하는 것이 아니라 이미지로 들어오는 빛을 역추적 하는 기법이라는 차이가 있습니다. 다른 렌더링 기법 대비 레이트레이싱의 장점은 매우 현실적인 그래픽을 렌더링 할 수 있다는 장점이 있습니다. 실제 현실의 물리계에서 일어나는 빛의 반사를 가장 직관적으로 구현한 기법이기 때문에 현실적인 그래픽을 만들 수 있습니다. 반면 단점은 이미지를 구성하기 위해 필요한 수 많은 광선 다발을 추적해야 하기 때문에 극도로 높은 컴퓨터 자원을 필요로 합니다. 그래서 레이트레이싱은 1980년대에 제안된 오래된 렌더링 기법이지만, 그동안은 매우 제한된 환경에서만 활용되어 왔습니다. 그래픽을 실시간으로 렌더링해야 하는 비디오 게임 등에서는 거의 사용되지 않았고, 미리 렌더링을 해서 보여 줄 수 있는 영화, 애니메이션 등에서 주로 활용되어 왔습니다. 하지만 현대 컴퓨터 하드웨어의 발전을 통해 가정용 컴퓨터에 들어가는 그래픽카드들이 레이트레이싱 전용 직접회로인 RT 코어를 탑재하며 실시간 렌더링을 필요로 하는 비디오 게임 등에서도 제한적으로 레이트레이싱 기법이 활용되고 있습니다. 아마 컴퓨터를 잘 모르시는 분들도 그래픽카드 모델명이 RTX3070이다, RTX4080이다 이런 말들을 들어 보셨을 텐데요, 이렇게 RTX 이름을 달고 있는 그래픽카드들이 바로 RT 코어를 내장하고 있는 그래픽카드들 입니다.

Figure 1. Control(2019)에서 구현된 실시간 레이트레이싱

초당 수십장의 프레임을 렌더링 하는 비디오 게임에서 사용되는 실시간 레이트레이싱 기법은 아직 부족한 점이 많음에도 불구하고, 2019년 출시된 비디오 게임인 “Control”에서 기존 렌더링 기법(왼쪽)과 실시간 레이트레이싱(오른쪽)을 비교해 보면 빛의 반사와 사물의 그림자에서 확연한 차이가 나는 것을 볼 수 있습니다. 이처럼 레이트레이싱은 빛이 반사되어 생기는 상, 가려서 생기는 그림자 등을 매우 현실적으로 렌더링 할 수 있는 기법입니다.

최근엔 많은 게임 엔진과 렌더링 엔진 등에서 레이트레이싱을 기본 옵션으로 제공하고 있어 손쉽게 구현이 가능합니다. 하지만 우리는 이번 프로젝트에서 python과 numpy등 기본적인 과학계산 라이브러리만을 이용하여 실제 레이트레이싱을 밑바닥부터 구현해 보도록 하겠습니다.

문제와 좌표계를 정의하기

흥미로운 주제가 정해 졌으니 이제 문제와 좌표계를 정의할 차례 입니다. 우리는 궁극적으로 레이트레이싱 기법을 이용하여 2D 이미지를 렌더링 하기를 원합니다. 2D 이미지를 렌더링 한다는 의미는, 이미지를 구성하는 픽셀들의 색을 “적절히” 칠한다는 것을 의미합니다. 그리고 우리는 각 픽셀들의 색이 그 픽셀로 들어온 광선으로부터 정의될 것이라는 사실을 알고 있습니다.

Figure 2. 레이트레이싱을 이용한 이미지 렌더링

위 그림에는 2D 이미지(프레임)인 Scene의 픽셀 $ P(a) $, $P(b)$, $P(c)$를 각각 통과하는 세개의 광선 $R(a)$, $R(b)$, $R(c)$이 그려져 있습니다. 광선 $R(a)$의 경우 정의된 물체인 파란색 구에서 반사되어 광원을 향하고 있습니다. 이 경우 우리는 픽셀 $P(a)$를 어떤 색으로 칠해야 할까요? 광선 $R(a)$가 파란색 구에 닿는 부분은 상대적으로 밝을 것이기 때문에 우리는 밝은 색을 칠해주면 됩니다. 그림에서는 $P(a)$의 색이 흰색으로 표기 되어 있습니다. 마찬가지로 픽셀 $P(b)$를 통과하는 광선 $R(b)$는 빛이 물체에 닿고 빈 공간 어딘가로 반사가 될 것입니다. 광원을 직접적으로 향하지 않기 때문에 픽셀 $P(b)$는 물체의 색인 파란색을 띄게 될 것입니다. 마지막으로 픽셀 $P(c)$를 지나는 광선 $R(c)$는 바닥 면에서 반사되어 어딘가로 반사가 될 것이지만, 광원이 물체에 가려져 있습니다. 이 경우에 물체의 그림자가 생기게 되는데, 광선 $R(c)$는 그림자가 생기는 위치를 향하고 있기 때문에 픽셀 $P(c)$는 어두운 색을 띄게 될 것입니다.

이렇게 레이트레이싱을 통한 렌더링을 구현하기 위해선 우리의 시점(카메라)로부터 Scene의 픽셀을 통과하는 각 광선들이 결국 물체의 어떤 부분에 부딪히는지를 계산하고, 이를 통해 각 픽셀의 색을 결정하면 됩니다. 문제를 정의해 보니 정말 간단하죠? 이렇게 렌더링의 대상이 되는 Scene() 클래스를 구성하는 컨스트럭터는 다음과 같습니다.

class Scene():
    def __init__(self,
                 width,
                 height,
                 objects):
        self.w = np.array(width)
        self.h = np.array(height)
        self.ratio = width / height
        self.objects = objects
        self.image = np.zeros((height, width, 3))

광선 벡터

우리는 이미지를 구성하는 픽셀의 수 만큼 광선을 추적 해야 합니다. 만약 1920×1080 해상도의 이미지(scene) 한 장을 렌더링 한다고 가정하면 총 2,073,600개의 광선을 정의하고 추적해야 합니다. 이러한 광선들은 시작점과 방향이 있는 객체들로 정의하고 구현 할 수 있는데요. 문제는 각 광선들이 향하는 방향이 모두 다르다는 것 입니다.

그래서 우리는 시점(카메라의 위치)으로부터 2D 이미지의 각 픽셀들을 통과하는 광선의 공간 벡터의 방향을 계산해야 합니다. 카메라의 위치 $\vec{C_0}(x,y,z)$와 방향 $\vec{C_d}(x,y,z)$, 카메라의 시야각($ \text{FOV}(\theta) $)이 정해지면 각 픽셀을 통과하는 광선들의 공간 벡터의 방향을 계산 할 수 있습니다. 물론 카메라는 렌즈를 통과하는 회전축을 중심으로 회전(roll)이 가능한데, 이 경우는 카메라의 위쪽이 항상 $\hat{z}(0,0,1)$ 방향을 향한다고 가정하여 카메라의 roll 방향 회전은 고려하지 않겠습니다.

Figure 3. 이미지의 각 픽셀을 통과하는 광선 벡터의 방향 계산

카메라로부터 뻗어나가는 광선 벡터를 프로그래밍으로 구현하기 전에 먼저 사고 실험을 통해 어떤 모습의 이미지가 렌더링 될지 예상 해 보겠습니다. 텅 빈 공간 가운데 아주 넓은 평면이 있고, 우리가 그 평면 위에 서서 카메라로 사진을 찍어 본다고 가정해 보겠습니다. 그럼 어떤 사진이 찍혔을까요? 아마 예시로 가져온 오른쪽 달 사진처럼 멀리까지 뻗어있는 지평선이 보이는 사진이 촬영되었을 것입니다. 지평선이 사진의 정 가운데에 있다고 해 보면 이미지의 절반 아래쪽의 픽셀을 통과하는 광선 벡터들은 평면(예시에선 달 표면)을 향할테고, 이미지의 절반 위쪽의 픽셀을 통과하는 광선 벡터들은 어디에도 부딪히지 않은채 텅 빈 공간(예시에선 우주 공간)으로 날아가게 될 것입니다.

그렇다면 각 픽셀들은 어떤 색을 가질까요? 평면에 부딪히는 빛에 해당하는 픽셀 $P_1$은 평면의 색(흰색)을 가지게 될 것이고, 어디에도 부딪히지 않고 텅 빈 공간으로 날아가는 빛에 해당하는 픽셀 ($P_2$)는 도달한 빛이 없으므로 검은 색을 가지게 될 것입니다. 이제 실제로 이 사고 실험을 그대로 컴퓨터 프로그래밍을 통해 구현해 보겠습니다. 결과는 다음과 같습니다.

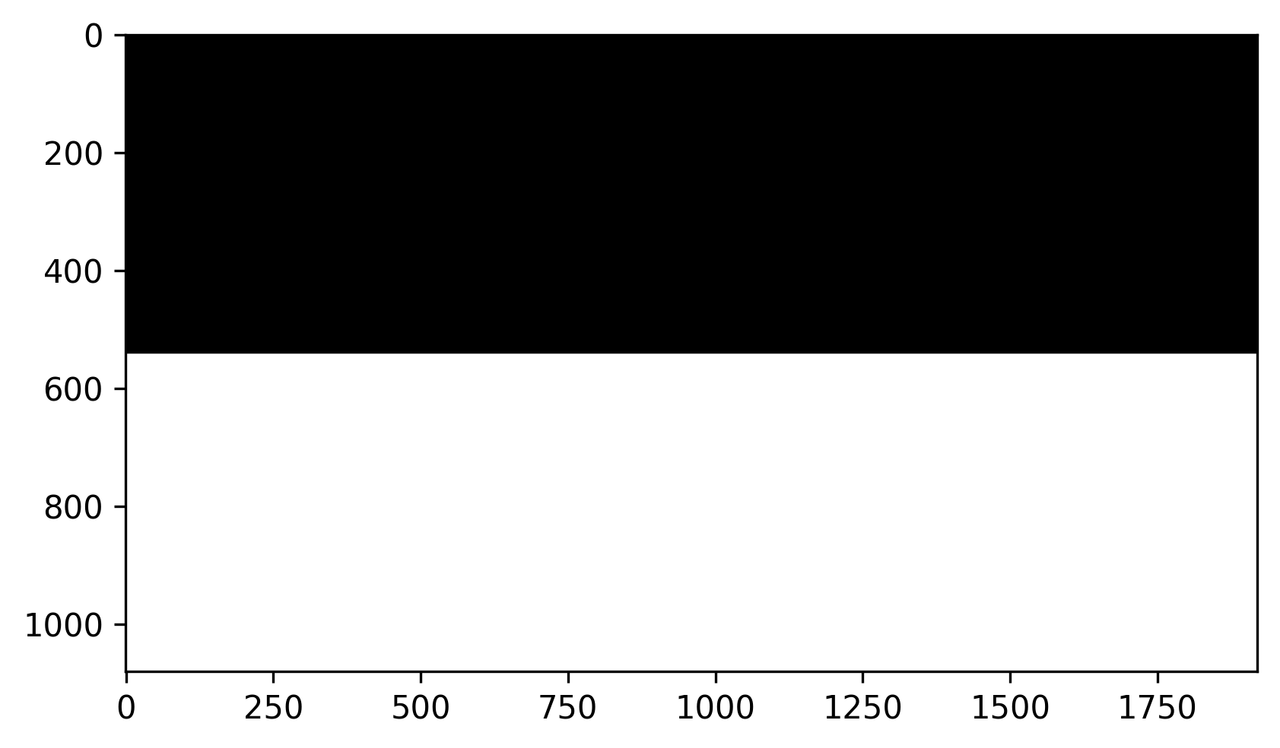Figure 4. 레이트레이싱을 통해 렌더링한 평면

그냥 검은색 절반, 흰색 절반 칠한거 아니냐구요? 아닙니다… 😅 이것은 흰색 지평선 입니다 …

지금 보고 계신 이미지는 1920×1080 해상도를 렌더링하기 위해 카메라로부터 뻗어나가는 2,073,600개의 광선을 정의하고, 해당 광선들이 각각 어디에 부딪히는지를 전부 추적하여 계산된 이미지입니다. 아래로 뻗어나간 광선 벡터는 흰색 평면에 닿았고, 위로 뻗어나간 광선 벡터는 텅 빈 검은 공간을 향하고 있습니다. 이제 코드를 보면서 구현된 레이트레이싱 기법을 이해해 보겠습니다.

먼저 Scene을 구성하는 object들을 정의해 보겠습니다. 앞으로 다양한 물체들의 클래스를 정의할 것 같지만, 여기서는 평면을 나타내는 Plane() 클래스를 만들어 보겠습니다. 구현 방식에 따라 다른데 저는 계산을 담당하는 레이트레이싱 알고리즘은 모두 Scene() 클래스에 넣을 것이기 때문에, Plane() 클래스에서는 이게 어떤 평면인지를 나타내 줄 수 있는 정보만 넣어 주면 충분 할 것 같습니다. 3차원 공간에서 평면은 한 점과 평면에 수직인 방향벡터(이를 보통 노말 벡터 라고 합니다)로 정의 할 수 있습니다. 그래서 Plane() 클래스 속성으로 .position, .normal 그리고 평면의 색을 정의하는 .color 속성을 정의합니다.

class Plane():
    def __init__(self, position, normal, color):
        self.type = 'plane'
        self.position = np.array(position)
        self.normal = normalize(np.array(normal))
        self.color = np.array(color)

위에서 사용되는 전역 함수 normalize()는 주어진 벡터를 유닛 벡터로 변환하는 함수로 다음과 같이 정의해 주었습니다.

def normalize(vector):
    return vector / np.linalg.norm(vector)

이제 Plane() 클래스를 이용하여 점 $P=(0,0,-1)$을 지나고, $\hat{z}$ 방향에 수직(즉, 노말 벡터가 $N=(0,0,1)$)인 흰색 평면을 만들어 보겠습니다. 만들어진 흰색 평면 white_plane을 1920×1080 해상도의 Scene에 넣고, Scene을 렌더링 하기 위한 시점(카메라)을 정의합니다. 카메라는 공간상에서 원점($C_0=(0,0,0)$)에 존재하고, $\hat{y}$ 축을 바라보고($C_d=(0,1,0)$) 있습니다.

white_plane = Plane(position=(0,0,-1), normal=(0,0,1), color=(1,1,1))

scene = Scene(width=1920, height=1080, objects=[white_plane])
scene.add_camera(camera_position=(0,0,0), camera_direction=(0,1,0))
scene.render()
scene.draw()

이제 직관적으로 각 객체들이 어떻게 어울리는지 이해하셨을 거라고 생각 됩니다. scene 객체를 만든 후, 해당 scene 내에 물체(white_plane)와 카메라를 배치하고(.add_camera()), 해당 카메라로 사진을 찍고(.render()), 이미지를 출력한다고(.draw()) 생각하시면 직관적일것 같습니다. 이미 섹션이 너무 길어졌네요. 이번 섹션에서는 광선 벡터의 방향($ D $)을 이해하는 것이 목적이니 Scene() 클래스에서 .add_camera()와 .render() 메서드를 살펴 보도록 하겠습니다.

.add_camera() 메서드는 Figure 3에서 정의한 카메라의 기본적인 속성들을 갖고 있습니다. 아직 depth_limit에 대해선 설명하지 않았는데, 이후에 하도록 하겠습니다.

    def add_camera(self,
                   camera_position,
                   camera_direction,
                   depth_limit = 3):
        self.Co = np.array(camera_position)
        self.Cd = normalize(np.array(camera_direction) - self.Co)
        self.Cu = np.array([0,0,1])
        self.Cr = normalize(np.cross(self.Cd, self.Cu))
        self.hFOV = 75
        self.depth_limit = depth_limit
        self.pixel_w = 2*np.tan(np.radians(self.hFOV/2)) / self.w
        self.pixel_h = self.pixel_w

우리는 .render() 메서드를 통해 scene에 추가된 카메라의 원점(Co)에서 출발하여 이미지의 픽셀 (x,y)를 향하는 광선의 방향 벡터 $ D $ 를 계산합니다. 카메라의 렌즈가 향하는 방향(Cd)으로부터 변위 (dx, dy)를 계산하여 광선의 방향 벡터 $ D $를 결정한다고 이해하시면 되겠습니다.

    def render(self):
        for x in range(self.w):
            for y in range(self.h):
                dx = self.pixel_w * (x - self.w/2)
                dy = - self.pixel_h * (y - self.h/2)
    
                O = self.Co # Origin of ray
                D = normalize(self.Cd + dx*self.Cr + dy*self.Cu) # Direction of ray
    
                color = self.trace(O, D)
                self.image[y,x] = np.clip(color, 0, 1)

이렇게 뻗어나간 광선은 시작점($O$)과 방향($D$)을 갖고 있습니다. 마지막으로 이렇게 모든 색을 다 채워넣은 .image를 .draw() 메서드를 이용해 시각화 합니다.

    def draw(self, dpi=300):
        plt.figure(dpi=dpi)
        plt.imshow(self.image)
        plt.show()

다음 섹션에서는 이제 .trace() 메서드를 통해 해당 광선이 어떤 물체에 충돌하였는지 계산해 보겠습니다.

광선 벡터와 물체의 상호작용

먼저 우리는 카메라의 중심점 $O$로부터 방향 $D$를 갖고 뻗어나가는 각 광선이 처음으로 만나는 물체가 무엇인지 추적해야 합니다. .trace() 메서드는 다시 .intersection() 메서드를 호출하여 광선과 scene에 존재하는 각 물체들의 교차 좌표(intersection)와 거리(distance)를 계산하고, 가장 가까이 있는 물체와 그 거리를 계산합니다. 만약 최소 거리(min_distance)가 np.inf일 경우 해당 광선이 어떤 물체와도 부딪히지 않는다고 볼 수 있습니다.

    def trace(self, ray_origin, ray_direction):
        # Step 1: Find the closest object
        min_distance = np.inf
        closest_object = None
        M = None # closest intersection point
        for o, obj in enumerate(self.objects):
            distance, intersection = self.intersection(ray_origin, ray_direction, obj)
            if distance < min_distance:
                min_distance = distance
                closest_object = obj
                M = intersection
        if min_distance == np.inf: # no object
            return np.zeros(3)
    
        # Step 2: Get properties of the closest object
        color = closest_object.color
        # Step 3:
        return color

이렇게 각 광선이 처음으로 만나는 물체의 특징이 scene을 렌더링 할 때의 색을 결정합니다. 이후 우리가 다양한 기법을 적용하여 더 현실적은 그래픽을 렌더링 할 수 있지만, 여기서는 그냥 가장 가까운 물체의 색(closest_object.color)을 바로 적용해 보겠습니다.

.trace() 메서드의 핵심은 .intersection() 메서드를 호출하여 광선과 물체의 거리와 좌표를 계산하는데 있습니다. 그런데 조금 생각해 보시면 금방 이 부분이 그다지 간단하지 않다는 것을 알 수 있습니다. 같은 위치에 있다고 하더라도 평면, 구, 정육면체 등 물체의 모양이 다 다르고, 빛을 받는 면의 각도에 따라 거리와 좌표가 달라질 수 있기 때문입니다. 이제 우리는 이 문제를 풀기 위해 공간벡터를 이용하여 각 물체에 대해 정의하고, 벡터 계산을 통해 거리와 좌표를 계산해 보겠습니다.

Ray-Plane intersection

먼저 광선이 평면에 닿는 경우를 생각해 보겠습니다. 점 $O$로부터 방향 $D$를 갖고 나아가는 광선은 한쪽 방향으로 나아가는 직선으로 표현 할 수 있습니다. 직선에 속한 수많은 점들을 매개변수식으로 표현하면 다음과 같습니다.

\[O + tD\]

방향벡터 $D$의 크기는 1이므로 $t$는 점 $O$로부터의 거리가 될 것입니다. 광선은 한쪽 방향으로 뻗어나가니 $t>0$인 조건에서만 고려하면 되겠습니다.

이제 평면을 정의해 보겠습니다. 수학적으로 공간에 위치한 평면은 평면 상의 점 $P_0$를 포함하고, 노말 벡터 $N$에 수직인 점들로 표현 할 수 있습니다. 즉 평면 위의 임의의 벡터($P-P_0$)는 노말 벡터 $N$에 수직이므로, 평면을 매개변수 방정식으로 표현하면 다음과 같습니다.

\[(P-P_0) \cdot N = 0\]

직선 $O+tD$와 평면 $ (P-P_0) \cdot N = 0 $ 사이의 관계를 그림으로 나타내면 다음과 같습니다. 직선과 평면의 교차점을 $I$라고 할 때, I는 두 매개변수 방정식 $I=O+t_{I}D$와 $(I-P_0) \cdot N = 0$을 만족하게 됩니다.

Figure 5. Ray-Plane intersection

직선이 평면에 포함되거나 평행하지 않을 때(즉, $D \cdot N \neq 0$), 이를 만족하는 $t$는 다음과 같습니다.

\[t = \frac{(P_0 - O) \cdot N}{D \cdot N}\]

위 방정식을 통해 우리는 교차점의 좌표 $I$와 교차점까지의 거리 $t$를 계산 할 수 있습니다. .intersection() 메서드의 코드는 다음과 같습니다. $t$가 매우 큰 경우($ t > 10^4$), 우리는 광선이 평면을 지나지 않는다고(평면과 평행하다고) 볼 수 있습니다. 이런 경우 교차점까지의 거리는 np.inf가 됩니다. 마찬가지로 $t$ 가 음수인 경우($ t < 0 $) 역시 광선이 반대 방향으로 날아가기 때문에 평면과 만나지 않는다고 볼 수 있습니다.

    def intersection(self, ray_origin, ray_direction, object):
        if object.type == 'plane':
            # Ray-Plane intersection
            O = ray_origin
            D = ray_direction
            P0 = object.position
            N = object.normal
    
            t = np.dot((P0-O), N) / np.dot(D, N)
            if t > 10e4 or t < 0:
                distance = np.inf
            else:
                distance = t
            intersection = O + distance*ray_direction
            return distance, intersection

이렇게 광선과 평면의 공간 벡터를 이용하여 평면이 카메라 상에서 어떻게 보이는지 계산해 보았습니다. 위 코드를 이용해 scene을 렌더링 하면 Figure 4와 같은 결과를 볼 수 있습니다. 하지만 Figure 4에서 보실 수 있다 시피 단색 컬러를 입힌 평면은 그렇게 공간감이 느껴지지 않습니다. 위에서 만든 Plane() 클래스를 조금 응용하여 체커보드 객체를 생성하는 Checkerboard() 클래스를 만들 수 있습니다.

Checkerboard() 클래스는 xy 평면 상에서 검은색과 흰색 타일이 반복적으로 놓인 구조입니다. 다시 말해 평면 위 점의 위치에 따라 객체의 .color 속성이 달라져야 합니다. 따라서 .color 속성을 동적으로 바꿔 줄 수 있는 .colorize() 메서드를 추가하여 Checkerboard() 클래스를 구성합니다.

class Checkerboard():
    def __init__(self, position, normal):
        self.type = 'checkerboard'
        self.position = np.array(position)
        self.normal = normalize(np.array(normal))

    def colorize(self, color):
        self.color = color

이제 .intersection() 메서드에 광선이 물체에 닿는 교차점의 좌표 $I$에 따라 Checkerboard() 클래스의 .colorize() 메서드를 호출 할 수 있는 분기를 넣습니다. 교차점(intersection)의 xy 좌표에 따라 Checkerboard() 클래스의 .color 속성을 흰색(np.ones(3)) 혹은 검정색(np.zeros(3))으로 업데이트 해 줍니다.

    def intersection(self, ray_origin, ray_direction, object):
        if object.type == 'plane' or object.type == 'checkerboard':
            # Ray-Plane intersection
            O = ray_origin
            D = ray_direction
            P = object.position
            N = object.normal
    
            distance = np.dot((P-O), N) / np.dot(D, N)
            if distance > 10e4 or distance < 0:
                distance = np.inf
            intersection = O + distance*ray_direction
    
            if object.type == 'checkerboard':
                if distance != np.inf:
                    if np.floor(intersection[0]) % 2 == np.floor(intersection[1]) % 2:
                        color = np.ones(3)
                    else:
                        color = np.zeros(3)
                    object.colorize(color)
    
            return distance, intersection

이제 Figure 4에서 그린 흰색 평면 대신 같은 위치에 checkerboard 객체를 생성하여 scene을 렌더링 합니다.

checkerboard = Checkerboard(position=(0,0,-1), normal=(0,0,1))

scene = Scene(width=1920, height=1080, objects=[checkerboard])
scene.add_camera(camera_position=(0,0,0), camera_direction=(0,1,0))
scene.render()
scene.draw()

결과는 다음과 같습니다. 어떤가요? 실제로 카메라를 통해 공간 상에 위치한 평면을 렌더링 했다는 것이 잘 느껴지시죠? 이제 더 다양한 물체를 구현하여 scene에 추가해 보도록 하겠습니다.

Figure 6. Ray-Plane intersection을 이용해 렌더링 된 체커보드 객체

Ray-Sphere intersection

평면 다음으로 구현해 볼 물체는 바로 구(Sphere) 입니다. 공간 상에서 구는 구의 중점($P_0$)과 반지름($R$)로 표현 됩니다. 공간 상에서 구 객체를 생성하기 위한 Sphere() 클래스는 다음과 같습니다. 중점과 반지름에 대한 속성을 갖고 있습니다.

class Sphere():
    def __init__(self, position, radius, color):
        self.type = 'sphere'
        self.position = position
        self.radius = radius
        self.color = np.array(color)

그렇다면 이러한 구 객체는 광선 벡터와 어떻게 상호작용 할까요? 우리는 평면과 마찬가지로 구의 점들을 매개변수 방정식으로 표현 할 수 있습니다. 구에 속한 임의의 점($P$)은 구의 중점 $P_0$로부터 반지름 $R$ 만큼 떨어져 있으므로 다음 식을 만족합니다.

\[\lvert P-P_0 \rvert ^2 - R^2 = 0\]

만약 광선($O+tD$)가 구를 지난다면, 조건에 따라 다음과 같은 경우가 발생 할 수 있습니다. 광선은 구를 뚫고 지나가는 경우가 있을 수 있고, 이 경우엔 광선과 구 사이의 교차점은 2개가 발생합니다. 이를 각각 $I_1$과 $I_2$라 할 수 있습니다. 광선이 구의 면을 정확하게 지나 하나의 교차점을 갖는 경우, 즉 $I_1=I_2$인 경우와 광선이 구를 지나지 않는 경우가 있을 수 있습니다. 이 경우엔 교차점을 찾을 수 없습니다.

Figure 7. Ray-Sphere intersection

오른쪽 그림에서 광선의 매개변수 $t$의 조건에 따라 교차점이 어떤 식으로 정의 되는지 볼 수 있습니다. 이제 매개변수 방정식을 풀어 실제 교차점 $I$의 좌표와 교차점 까지의 거리 $t$를 계산해 보겠습니다. 광선이 구를 지나는 경우 구 위의 점 $P$를 광선의 매개변수 식인 $O+tD$로 치환 할 수 있습니다.

\[\lvert O+tD -P_0 \rvert ^2 - R^2 = 0\]

위 식을 풀어 쓰면 다음과 같습니다.

\[D^2 t^2 + 2D(O-P_0) t + \lvert O-P_0 \rvert ^2 - R^2 = 0\]

해당 식을 자세히 보면 $t$에 대한 2차 방정식인 것을 볼 수 있습니다. 이 2차 방정식의 실수해에 따라 광선과 구의 관계가 결정 됩니다. 두 개의 실수 해가 존재할 경우는 광선이 구를 뚫고 지나가 두 교차점 $I_1$과 $I_2$가 생기는 경우이며, 하나의 실수해가 존재하는 경우 광선이 구의 면을 정확하게 지나 하나의 교차점을 갖는 경우, 마지막으로 해가 존재하지 않는 경우 광선은 구를 지나지 않습니다.

2차 방정식을 푸는 방법은 잘 알고 계신 근의 공식을 이용하는 것 입니다. 이때 근의 공식 속 판별식(Discriminant)의 부호에 따라 실수해의 조건이 결정됩니다. 매개변수 방정식의 실수해 $t$는 다음과 같습니다.

\[t=\frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

방정식의 다항계수 $a$, $b$, $c$는 각각 다음과 같습니다.

\[\begin{aligned} a&=D^2 \\ b&=2D(O-P_0) \\ c&=\lvert O-P_0 \rvert ^2 - R^2 \end{aligned}\]

우리는 판별식 $b^2 - 4ac$의 부호에 따라 실수해의 조건을 판정합니다. .intersection() 메서드에 object의 .type 속성이 'sphere'인 분기를 넣어 광선과 구의 교차점의 좌표와 거리를 계산합니다. 이때 $b^2 - 4ac>0$인 경우 광선은 구 위의 두 교차점 $I_1$과 $I_2$를 지나므로 광선에서 먼저 닿는 교차점, 즉 매개변수 $t$가 더 작은 교차점을 판단하는 분기문을 넣습니다.

        if object.type == 'sphere':
            # Ray-Sphere intersection
            O = ray_origin
            D = ray_direction
            P0 = object.position
            R = object.radius

            a = np.dot(D, D) # always 1
            b = 2 * np.dot(D, O - P0)
            c = np.dot(O - P0, O - P0) - R * R
            discriminant = b * b - 4 * a * c
            if discriminant > 0: # two roots
                t1 = (-b + np.sqrt(discriminant)) / (2.0*a)
                t2 = (-b - np.sqrt(discriminant)) / (2.0*a)

                if t1 > 0 and t2 > 0:     # find closest intersection
                    distance = np.min([t1, t2])
                elif t1 <= 0 and t2 <= 0: # no intersection
                    distance = np.inf
                else:
                    distance = np.max([t1, t2])

            elif discriminant == 0: # one root
                t = -b/(2*a)
                distance = t

            elif discriminant < 0: # no root
                distance = np.inf

            intersection = O + distance*ray_direction
            return distance, intersection

이제 Sphere() 클래스를 이용하여 scene 상에 빨간색, 초록색, 파란색 구를 추가해 보도록 하겠습니다. 이전에 미리 정의해 둔 체커보드는 $z=-1$인 평면이므로, 해당 평면 위에 구를 올리기 위해 각 구의 중심점(position)의 좌표를 $z=-1+r$로 정의해 주었습니다.

checkerboard = Checkerboard(position=(0,0,-1), normal=(0,0,1))
red_ball = Sphere(position=(0.0, 5, -1+0.8), radius=0.8, color=(1,0,0))
blue_ball = Sphere(position=(1.0, 4, -1+0.5), radius=0.5, color=(0,0,1))
green_ball = Sphere(position=(-1.0, 4.5, -1+0.3), radius=0.3, color=(0,1,0))

scene = Scene(width=1920, height=1080, objects=[checkerboard, red_ball, blue_ball, green_ball])
scene.add_camera(camera_position=(0,0,0), camera_direction=(0,1,0))
scene.render()
scene.draw()

위 코드를 통해 scene을 렌더링한 결과는 다음과 같습니다.

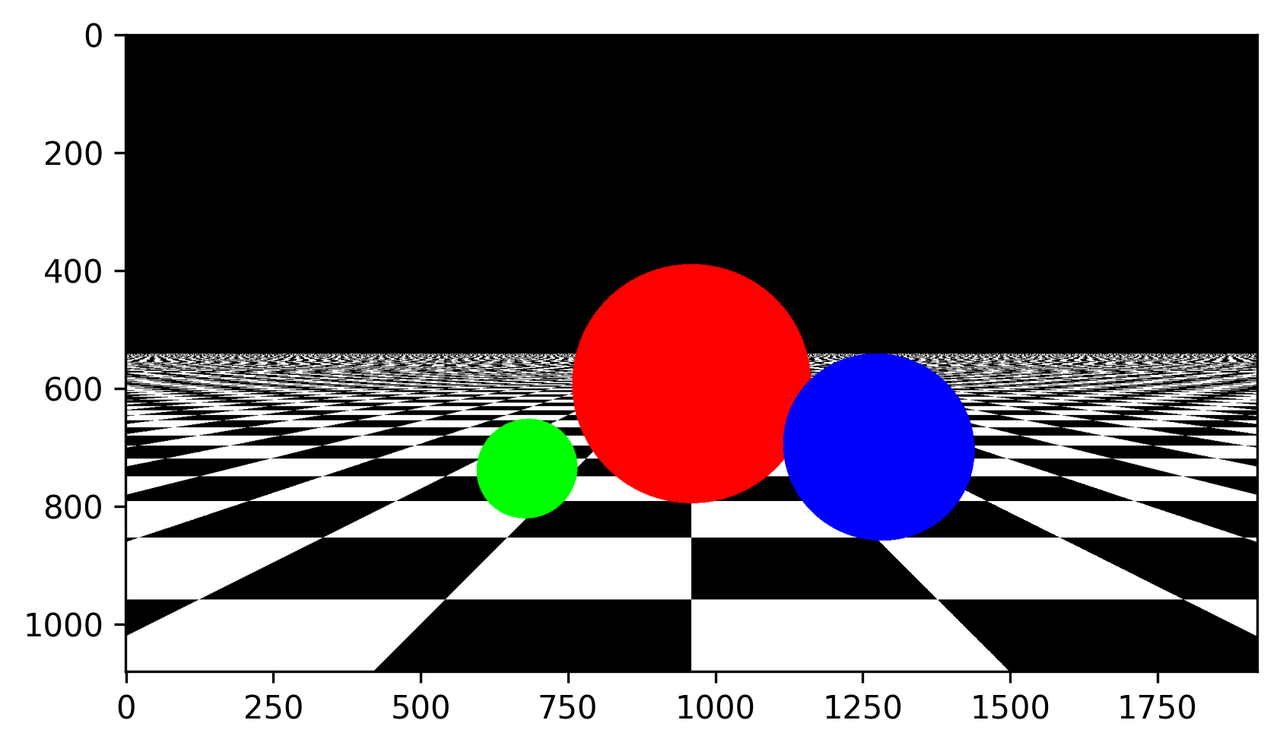Figure 8. Ray-Sphere intersection을 이용한 구 객체의 렌더링

조명 모델

지금까지 우리는 3차원 공간을 구성하고, 공간에 있는 여러 물체를 수학적으로 정의하고, 각 물체들이 카메라를 통해 어떻게 보일지 광선과 물체 사이의 매개변수 방정식을 풀어 계산해 보았습니다. 여기까지 잘 따라오셨나요? 만약 아직 여기까지 구현하지 못했다면 잠시 읽기를 멈추고 차근차근 따라해 보시기 바랍니다.

여러분들이 구현한 그래픽은 [그림 4]에 비해 대단히 발전되었지만, 지금까지 광선이란 단어를 사용해 온 것이 무색하게 아직 빛에 대한 내용은 들어가 있지 않습니다. 요컨대 빛이 물체와 상호작용하며 생기는 반사나 그림자 등이 구현되지 않은 상태입니다. 우리는 이제 조명 모델을 이용하여 광원에 의한 빛의 반사가 어떻게 물체의 색을 결정하는지 알아보도록 하겠습니다.

현재에도 널리 사용되는 조명 모델인 Phong 반사 모델은 컴퓨터 과학자 Bui Tuong Phong이 1975년 출판한 본인의 박사학위 논문에서 처음 소개되었습니다. Phong 반사 모델은 최종적으로 렌더링된 물체의 색을 세 개의 요소로 나누어 설명합니다. 각각 주변광(Ambient), 확산광(Diffuse), 반사광(Specular) 입니다. 사실 컴퓨터 그래픽스에서는 그냥 앰비언트, 디퓨즈, 스페큘러라고 부르는 것이 보통이지만, 저는 최대한 우리말을 써 보도록 하겠습니다.

Figure 9. Phong reflecion model을 이용하여 물체에 반사되는 다양한 빛을 고려 할 수 있다.

위 그림은 Phong 반사 모델의 세 요소를 도식화한 그림입니다. 보시는 것과 같이 물체의 최종 색을 결정하는 광량이 주변광(Ambient), 확산광(Diffuse), 그리고 반사광(Specular)의 합으로 결정되는 것을 볼 수 있습니다. 이제 각각의 빛에 대해 간단히 알아보도록 하겠습니다.

주변광(Ambient)

주변광은 요즘 인테리어에서 많이 쓰이는 간접 조명에 해당합니다. 여러분들이 어두운 방에서 플래시 켜고 물체를 직접 비추면 여러분은 물체에서 반사된 빛과 물체 반대쪽에 생기는 그림자를 쉽게 볼 수 있을 것입니다. 하지만 약한 간접조명에 의해 물체를 보게 될 경우 빛의 방향성이 명확하지 않기 때문에 그림자가 발생하지 않고 물체를 볼 수 있게 됩니다. 이처럼 주변광에 의한 색 표현은 명확한 광원으로부터 직접적으로 발사된 광선에 의한 색이 아니라, 공간 내의 다양한 주변 물체에서 반사되는 빛에 의한 색 표현 입니다. 위 그림에서 볼 수 있듯 주변광에 의한 색 표현은 방향성이 없고, 따라서 그림자가 생기지 않습니다. 만약 우리가 주변광을 고려하지 않는다면 광원에 의해 직접 조명이 닿지 않는 부분은 렌더링 할 수 없게 됩니다.

현실 세계에서는 빛은 수많은 물체에 의해 반사되며 방향성을 잃는 간접조명이 생기지만, 우리가 구현하고 있는 시뮬레이션 공간에서는 다양한 주변 물체에서 반사되는 빛, 즉 간접조명이 없습니다. 만약 다양한 물체가 있다고 하더라도 간접 조명을 직접 조명의 무수한 반사로 계산하는 것은 매우 비효율적입니다. 따라서 컴퓨터 그래픽스에서 주변광을 모델링 할 때는 공간에 은은하게 공기처럼 깔린(?) 주변광을 명시합니다.

확산광(Diffuse)

확산광과 반사광은 모두 직접 조명에 의한 색 표현 입니다. 따라서 해당 색 표현을 만든 광원이 존재하고, 광원의 방향에 따라 그림자가 발생합니다. 확산광은 물체 표면에서 일어나는 빛의 난반사에 의해 결정되는 색 표현 입니다. 이는 실제로 우리가 보게 되는 물체의 색을 대부분 결정하는 요소로, 만약 물체가 거울과 같이 이상적으로 매끈하여 정반사만 일어난다면, 우리는 광원이 적절한 각도에 배치 될 때만 물체를 볼 수 있게 됩니다. (그리고 매우 눈이 부시겠지요! 🤩)

반사광(Specular)

마지막으로 반사광은 직접 조명이 물체의 표면에서 정반사되며 나타나는 색 표현 입니다. 위 그림에서 쉽게 볼 수 있듯 반사광이 추가되면 우리는 물체의 표면이 매끈하다고 느낍니다. 정반사 라는 것이 곧 매끈한 물체의 표면에서 일어나는 현상이기 때문에 이러한 인지는 당연하다고 볼 수 있겠네요.

Phong 반사 모델

이제 각 빛의 요소를 담은 Phong 반사 모델을 수학적으로 구현해 보도록 하겠습니다. 물체의 최종적인 색은 다음과 같이 계산 됩니다.

\[I_p = k_{a}I_{a} + \sum_{l \in \text{lights}} (k_{d}(\hat{L}_l \cdot \hat{N})I_{l,d} + k_{s}(\hat{R}_l \cdot \hat{V})^\alpha I_{l,s})\]

이제 수식을 풀어서 설명해 보도록 하겠습니다. 광원 $l$이 하나일 경우, Phong 반사 모델을 이용해 계산 되는 물체의 최종적인 색 $I_p$은 첫번째 항인 주변광($k_{a}I_{a}$), 두번째 항인 확산광($k_d (\hat{L} \cdot \hat{N}) I_d$), 그리고 마지막 항인 반사광($k_s (\hat{R} \cdot \hat{V})^\alpha I_s$)의 합으로 결정 됩니다. 빛의 위치에 따라 결정되는 확산광과 반사광의 경우 scene에 광원 $l$이 여러개 있을 수 있어 $\Sigma$ 항을 통해 이를 모두 더해주는 모습입니다.

각 항의 계수 $k_a$, $k_d$, $k_s$는 0부터 1사이의 값으로 각각 주변광, 확산광, 반사광의 상대적인 크기를 결정합니다. 각 항에 곱해지는 $I_a$, $I_d$, $I_s$는 각각 주변광, 확산광, 반사광으로부터 발현되는 색을 결정합니다. 물체의 색은빛의 3원색인 빨간색, 초록색, 파란색에 의해 표현되므로 우리는 모든 $I$ 값을 (R,G,B) 벡터 형태로 계산합니다.

Figure 10. Phong reflecion model에 작용하는 방향 벡터

마지막으로 확산광과 반사광은 광원의 방향 $\hat{L}$, 물체의 노말 벡터 $\hat{N}$, 카메라의 방향 $\hat{V}$, 마지막으로 빛이 물체에 반사되어 나가는 반사각의 방향을 나타내는 반사 벡터 $\hat{R}$을 고려하여 크기가 결정 됩니다. 시간을 들여 조금 생각해 보시면 왜 확산광의 크기가 $(\hat{L}_l \cdot \hat{N})$에 비례하는지, 반사광의 크기가 $(\hat{R}_l \cdot \hat{V})$에 의해 결정되는지 직관적으로 이해 하실 수 있을 거라고 생각 합니다. 내적을 이루는 두 벡터가 수직인 경우 내적의 값이 0이 되는데, 광원에 비치는 물체 표면의 각도에 따라 우리 눈에 어떤 색으로 보일지 생각해 보시면 좋을것 같아요.

여기까지 우리는 Phong 반사 모델에서 사용되는 세 요소를 수학적으로 정의해 보았습니다. 이제 프로그래밍을 구현을 할 차례… 인데요. 최근에는 Phong 반사 모델을 사용하는 것 보다 NASA 제트추진연구소(JPL)의 컴퓨터 그래픽스 엔지니어 Jim Blinn이 이를 개선한 버전인 Blinn-Phong 반사 모델을 주로 사용합니다. 이는 매번 반사 벡터 $\hat{R}$을 계산하는 것이 다소 비효율적이기 때문인데요. 우리는 반사광의 크기를 결정하는 반사 벡터 $\hat{R}$과 카메라의 방향 벡터 $\hat{V}$의 내적 $(\hat{R}_l \cdot \hat{V})$을 노말 벡터 $\hat{N}$과 하프 벡터 $\hat{H}$의 내적인 $(\hat{N} \cdot \hat{H})$로 대체 할 수 있습니다. 하프 벡터 $\hat{H}$는 광원의 방향 벡터 $\hat{L}$와 카메라의 방향 벡터 $\hat{V}$의 중간 방향을 가리키는 벡터인 $ \frac{\hat{L}+\hat{V}}{\lvert \hat{L}+\hat{V} \rvert} $로 정의 됩니다.

Blinn-Phong 반사 모델의 구현

이제 우리는 수학적으로 정의된 Blinn-Phong 반사 모델을 파이썬을 통해 구현합니다. 물체에 비춰지는 확산광과 반사광을 구현하기 위해 우리는 광원과 빛이 물체에 반사될때 교차점(intersection)의 노말 벡터 $N$이 필요합니다. Scene() 클래스에 광원을 추가하는 .add_light() 메서드와 노말 벡터를 반환하는 .get_normal() 메서드를 추가해 줍니다. 또한 각각 주변광과 반사광의 크기를 결정하는 계수 $k_a$와 지수 $\alpha$를 컨스트럭터에 추가합니다.

    def __init__(self,
                 width,
                 height,
                 objects):
        self.w = np.array(width)
        self.h = np.array(height)
        self.ratio = width / height
        self.objects = objects
        self.image = np.zeros((height, width, 3))
        self.ka = 0.05
        self.alpha = 30
        
    def add_light(self, light_position, light_color = (1,1,1)):
        self.Lo = np.array(light_position)
        self.Lc = np.array(light_color)
    
    def get_normal(self, intersection, object):
        if object.type == 'plane' or object.type == 'checkerboard':
            return object.normal
        elif object.type == 'sphere':
            return normalize(intersection - object.position)

여러분들은 .add_light() 메서드를 수정하여 현실 세계에 있는 다양한 광원을 구현할 수 있습니다. 빛이 강한 방향성을 갖고, 좁은 공간을 비추는 스팟라이트를 구현 해 볼 수도 있고, 점광원을 응용하여 면광원을 구성 할 수도 있습니다. 여기서는 간단히 공간 상의 한 점(Lo)에서 흰색 빛이 방사형으로 퍼져 나가는 점광원을 구현해 보았습니다.

.get_normal() 메서드가 반환하는 노말 벡터의 경우 평면은 어느 점에서나 고정된 값을 가지기 때문에 Plane()이나 Checkerboard() 클래스의 경우 .normal 속성을 반환해 주면 되지만, Sphere() 클래스로 생성되는 객체들은 구의 중심점으로부터 교차점을 향하는 방향 벡터가 해당 물체의 노말 벡터가 됩니다. 이를 계산하여 반환해 줍시다.

다음으로 우리가 구현한 Plane(), Checkerboard(), Sphere() 클래스에 각각 확산광과 반사광의 크기를 결정하는 계수 $k_d$와 $k_s$를 속성으로 명시합니다.

class Plane():
    def __init__(self, position, normal, color, diffuse_k, specular_k):
        self.type = 'plane'
        self.position = np.array(position)
        self.normal = normalize(np.array(normal))
        self.color = np.array(color)
        self.kd = diffuse_k
        self.ks = specular_k

class Checkerboard():
    def __init__(self, position, normal, diffuse_k, specular_k):
        self.type = 'checkerboard'
        self.position = np.array(position)
        self.normal = normalize(np.array(normal))
        self.kd = diffuse_k
        self.ks = specular_k

    def colorize(self, color):
        self.color = color

class Sphere():
    def __init__(self, position, radius, color, diffuse_k, specular_k):
        self.type = 'sphere'
        self.position = position
        self.radius = radius
        self.color = np.array(color)
        self.kd = diffuse_k
        self.ks = specular_k

이제 Scene() 클래스에서 광선 벡터의 궤적을 추적하는 .trace() 메서드 내에서 그림자와 Blinn-Phong 반사 모델을 구현합니다.

    def trace(self, ray_origin, ray_direction):
        # Step 1: Find the closest object
        min_distance = np.inf
        closest_object = None
        closest_object_idx = None
        closest_intersection = None # closest intersection point
        for o, obj in enumerate(self.objects):
            distance, intersection = self.intersection(ray_origin, ray_direction, obj)
            if distance < min_distance:
                min_distance = distance
                closest_object = obj
                closest_object_idx = o
                closest_intersection = intersection
        if min_distance == np.inf: # no object
            return np.zeros(3)

        # Step 2: Get properties of the closest object
        ambient_color = closest_object.color
        diffuse_color = closest_object.color
        specular_color = self.Lc
        N = self.get_normal(closest_intersection, closest_object)
        L = normalize(self.Lo - closest_intersection)
        V = normalize(ray_origin - closest_intersection)
        H = normalize(L + V)

        # Step 3: Find if the intersection point is shadowed or not.
        distance_to_other_objects = []
        for o, obj in enumerate(self.objects):
            if o != closest_object_idx:
                distance, _ = self.intersection(closest_intersection + N * .0001,
                                                L,
                                                obj)
                distance_to_other_objects.append(distance)
        if np.min(distance_to_other_objects) < np.inf: # intersection point is shadowed
            return np.zeros(3)

        # Step 4: Apply Blinn-Phong reflection model
        # add ambient
        color = self.ka * ambient_color
        # add diffuse
        color += closest_object.kd * max(np.dot(N, L), 0) * diffuse_color  
        # add specular
        color += closest_object.ks * max(np.dot(N, H), 0) ** self.alpha * specular_color
        return color

위 코드를 통해 우리가 위에서 수학적으로 정의한 Blinn-Phong 반사 모델을 그대로 구현해 보았습니다. 여러분들이 위에서 수학적인 개념이 어떻게 코드로 구현되는지 주목해 주시기 바랍니다. 아직 그림자를 어떻게 구현하였는지 설명을 하지 않았는데요. 핵심은 교차점에서 광원을 향하는 방향 벡터 $\hat{L}$이 다른 물체에 가리는지 확인하는 것 입니다. 이를 위해 .intersection() 메서드를 호출하여 자기를 제외한 다른 물체와의 거리를 계산하고 분기문을 통해 제어합니다.

이제 scene에 포함될 물체를 정의하고, .add_light() 메서드를 이용해 광원을 추가하고, scene을 렌더링 해 보겠습니다. 각 물체의 물리적인 특성을 기술하기 위해 diffuse_k와 specular_k 속성을 추가하는 것에 주목해 주시기 바랍니다. 광원의 위치는 원점으로부터 $z+5$ 좌표에 있는 점광원을 추가해 주었습니다.

checkerboard = Checkerboard(position=(0,0,-1), normal=(0,0,1), diffuse_k=1.0, specular_k=0.5)
red_ball = Sphere(position=(0.0, 5, -1+0.8), radius=0.8, color=(1,0,0), diffuse_k=1.0, specular_k=1.0)
blue_ball = Sphere(position=(1.0, 4, -1+0.5), radius=0.5, color=(0,0,1), diffuse_k=1.0, specular_k=1.0)
green_ball = Sphere(position=(-1.0, 4.5, -1+0.3), radius=0.3, color=(0,1,0), diffuse_k=1.0, specular_k=1.0)

scene = Scene(width=1920, height=1080, objects=[checkerboard, red_ball, blue_ball, green_ball])
scene.add_camera(camera_position=(0,0,0), camera_direction=(0,1,0))
scene.add_light(light_position=(0,0,5), light_color=(1,1,1))
scene.render()
scene.draw()

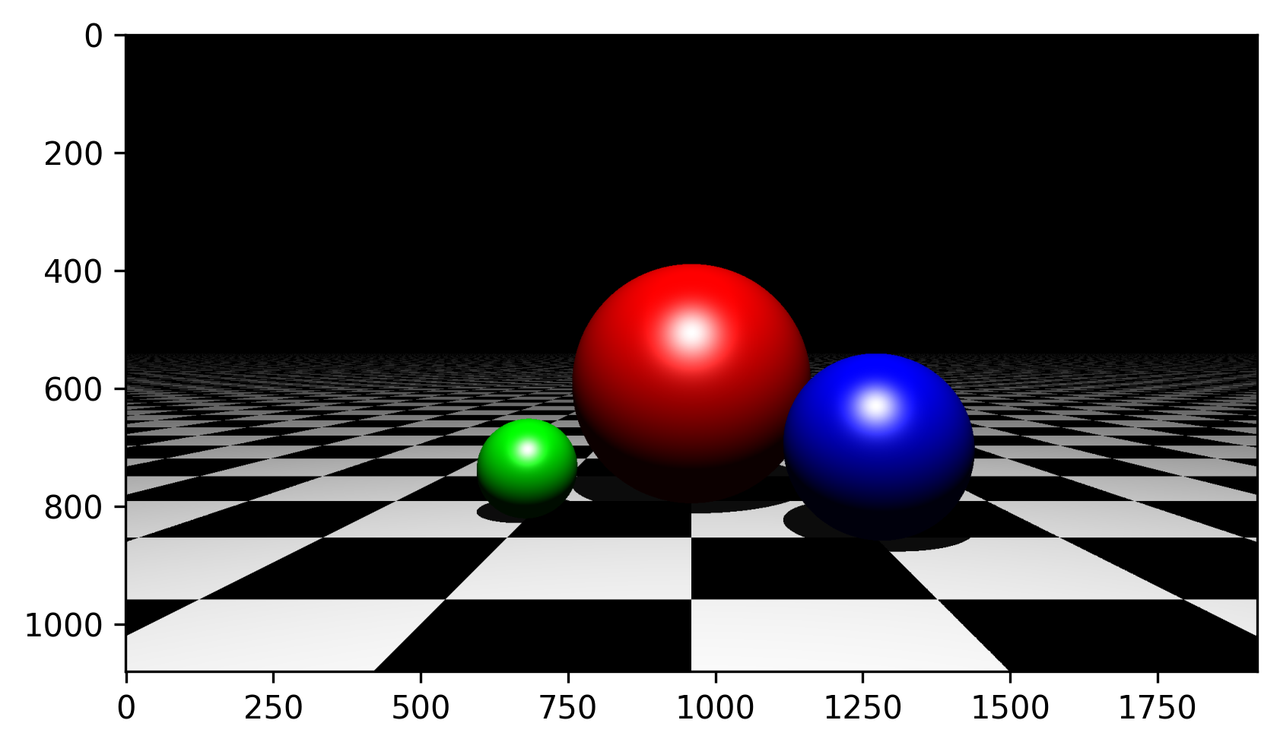Figure 11. Blinn-Phong reflecion model을 적용한 렌더링

결과를 보니 어떠신가요? 수학적으로 표현되는 빛을 모델링하니 현실적인 공간감이 느껴지는 3차원 scene을 렌더링 할 수 있었습니다. 그렇게 구현했으니 결과가 이렇다고 하면 당연한 이야기지만, 그래도 자연 현상을 설명하는 모델을 컴퓨터로 직접 구현해서 현실적인 결과를 눈으로 확인하는 일은 늘 굉장한 성취감을 주는 순간이라 생각합니다.

빛의 다중 반사

여기까지 잘 따라오셨나요? 정말 고생하셨습니다. 하지만 벌써 끝이라면 너무 아쉬운 일이겠죠? 😃 더욱 현실적인 레이트레이싱 기반의 렌더링을 위해 우리가 추가적으로 고려해야 하는 점은 빛의 다중 반사입니다. 우리 눈으로 들어오는 빛은 광원에서 출발하여 여러 물체에 반사되어 눈으로 들어오게 됩니다. 어릴적 거울 두개를 마주보고 가운데 물건을 놓아 보신 적이 있으신가요? 물체에 반사된 빛은 두 거울 사이에서 무한히 반사되어 여러개의 상을 만들게 됩니다. 거울은 빛의 반사율이 대단이 높은 물질이기 때문에 선명한 상을 만들지만, 반사율이 낮은 물질, 예를들어 저녁에 컴퓨터를 할 때 모니터에 비치는 여러분의 얼굴은 그렇게까지 선명하게 보이진 않죠. 그 빛은 모니터에 나와, 여러분의 얼굴에서 반사되고, 다시 모니터에 반사되어, 다시 여러분의 눈에 들어오게 됩니다. 즉 빛이 두번 반사된 것을 알 수 있습니다!

여러분의 눈으로 들어와 현실 세계를 렌더링하는 그래픽카드, 즉 광자는 현대 컴퓨터 하드웨어가 도저히 범접할 수 없는 성능을 가지고 있어 거의 무한히 반사되는 상도 실시간으로 렌더링 할 수 있습니다. 반면 우리가 레이트레이싱을 통해 두 거울 사이에서 무한히 반사되는 물체를 렌더링 하고자 한다면, 아무리 컴퓨터 하드웨어가 좋다고 하더라도 그야말로 무한한 시간이 걸리게 될 것입니다.

그래서 우리는 빛이 반사되는 최대 횟수(depth_limit)를 제한하여 빛의 다중 반사를 고려해 보겠습니다. 여기선 최대 반사 횟수를 3으로 제한하고 있지만, 여러분들은 다양한 숫자로 바꾸어 테스트 해 보시기 바랍니다. 단, depth_limit을 지나치게 높은 값으로 설정하는 경우 말씀 드렸다 시피 엄청난 연산 시간을 필요로 합니다.

빛의 다중 반사를 고려할 때의 핵심은 광선과 물체의 교차점(intersection)에서 입사된 광선의 입사각과 같은 반사각으로 다시 발사된다는 점입니다. 반사각의 방향 벡터 $R$은 이전 조명 모델에서 설명한 대로 $2(\hat{L} \cdot \hat{N})\hat{N}-\hat{L}$로 계산 됩니다. 이 경우엔 방향이 반대기 때문에 새롭게 발사되는 광선은 교차점 $I$에서 방향 $-R$로 나아갑니다. 반복문을 이용해 이를 연속적으로 계산하여 빛의 다중 반사를 계산 할 수 있습니다.

그렇다면 다중 반사에 의한 물체의 색은 어떻게 결정이 될까요? 이는 빛의 세기와 색을 곱한 값이 누적해서 더해지는 식으로 구현 할 수 있습니다. 물론 빛의 세기는 반사를 거듭하며 물체의 반사율에 따라 점점 감소하게 됩니다. 반사율이 0.5인 물체에 두번 반사되면 빛의 세기는 0.25가 되는 것이지요.

이제 .render() 메서드를 수정하여 빛의 다중 반사를 구현합니다. 코드를 보시면 .trace() 메서드를 호출하여 조명 모델을 통해 계산된 물체의 색(color) 이외에도 반사된 물체(object)와 교차점(intersection), 노말 벡터(N) 등이 함께 반환되는 것을 볼 수 있습니다. 그렇게 동작하도록 .trace() 메서드의 return 부분을 수정해 보시면 되겠습니다. 또한 빛의 세기를 나타내는 intensity가 물체의 반사율 속성(object.r)에 따라 지속적으로 감소되는 점을 볼 수 있습니다. 글이 너무 길어져서 따로 쓰지는 않겠지만, 물체를 생성하는 클래스에 반사율 속성(.r)을 명시해 주시면 되겠습니다.

마지막으로 새롭게 캐스팅되는 광선의 원점(O)과 방향(D)이 교차점과 노말 벡터를 통해 새롭게 계산되는 점을 확인 할 수 있습니다. 방향 벡터는 설명한 것과 같이 $-R$인 것을 볼 수 있지만, 새로운 광선의 원점(O)은 교차점(intersection)이 아니라 교차점으로부터 노말 벡터를 따라 아주 살짝 떨어진 지점, 즉 intersection + N * 0.001인 것을 볼 수 있는데요. 혹시 이유를 아시겠나요? 아까 설명하진 않았지만 그림자를 구현 할 때도 같은 트릭을 이용하였습니다.

    def render(self):
        for x in range(self.w):
            for y in range(self.h):
                dx = self.pixel_w * (x - self.w/2)
                dy = - self.pixel_h * (y - self.h/2)

                O = self.Co # Origin of ray
                D = normalize(self.Cd + dx*self.Cr + dy*self.Cu) # Direction of ray

                depth = 0
                intensity = 1.0
                base_color = np.zeros(3)
                while depth < self.depth_limit:
                    traced = self.trace(O, D)
                    if len(traced) < 4:
                        break
                    color, object, intersection, N = traced

                    O = intersection + N * .0001
                    D = normalize(D - 2 * np.dot(D, N) * N) # -R
                    base_color += intensity * color
                    intensity *= object.r
                    depth += 1
                self.image[y,x] = np.clip(base_color, 0, 1)

이제 반사율 속성을 가진 물체를 scene에 넣고 다시 렌더링 해 봅시다. 물체에 따라 반사율과 반사광 계수 $k_s$를 조절하였습니다.

checkerboard = Checkerboard(position=(0,0,-1), normal=(0,0,1), diffuse_k=1.0, specular_k=0.5, reflection=0.6)
red_ball = Sphere(position=(0.0, 5, -1+0.8), radius=0.8, color=(1,0,0), diffuse_k=1.0, specular_k=1.0, reflection=0.8)
blue_ball = Sphere(position=(1.0, 4, -1+0.5), radius=0.5, color=(0,0,1), diffuse_k=1.0, specular_k=0.4, reflection=0.4)
green_ball = Sphere(position=(-1.0, 4.5, -1+0.3), radius=0.3, color=(0,1,0), diffuse_k=1.0, specular_k=0.2, reflection=0.2)

scene = Scene(width=1920, height=1080, objects=[checkerboard, red_ball, blue_ball, green_ball])
scene.add_camera(camera_position=(0,0,0), camera_direction=(0,1,0), depth_limit=3)
scene.add_light(light_position=(0,0,5), light_color=(1,1,1))
scene.render()
scene.draw()

Figure 12. 빛의 다중 반사를 고려한 렌더링

결과에서 볼 수 있듯, 빛이 여러 물체에 반사되며 새로운 형태의 상을 만들고 더욱 현실적인 그래픽이라 느껴집니다. 준비한 이번 주차의 내용은 여기서 끝입니다. 여기까지 따라오시느라 정말 고생하셨습니다. 여러분들에게 주어지는 과제는 이 프로젝트를 따라서 마지막 최종 결과를 재현하는것 입니다. 여러분들이 직접 물체의 여러 물리적 특성과 위치를 바꾸어 가며 렌더링 해 보시기를 권장합니다. 결과를 재현하기 위한 모든 소스 코드는 이 프로젝트 페이지에 나와 있지만, 복사-붙여넣기 하여 실행 할 수 있는 전체 소스코드는 주어지지 않았습니다. 과제를 수행하며 이 프로젝트에 사용된 여러 개념을 이해하고 적용하시는 연습을 하실 수 있기를 기대합니다.

아래 도전 문제는 학습 목표 달성 등급인 A 평가를 받는데 영향을 주지 않지만, 이번 주차 과제의 A+는 도전 과제를 성공적으로 구현하신 분에게 드리도록 하겠습니다.

도전 문제: Ray-Box intersection을 이용하여 정육면체 구현하기

여러분은 이제 이 프로젝트를 응용하여 다양한 물체를 정의해 볼 수 있습니다. 예를 들어 거울 역할을 하는 객체를 만들기 위해 반사율이 대단히 높은 평면을 scene에 추가 해 볼 수 있고, 투명한 물체를 추가하기 위해 빛의 굴절(refraction)을 고려해 볼 수도 있습니다. 이번 주차의 도전 문제는 지금까지 배운 지식을 이용하여 scene에 정육면체를 추가하는 것 입니다. 정육면체는 노말 벡터가 고정이기 때문에 평면과 유사한 특징을 갖지만 제한된 크기를 가졌기 때문에 광선에 의한 교차점을 갖는 조건을 찾는 것이 상당히 까다롭습니다. “Ray-Box intersection”을 검색 하시면 다양한 참고 문헌이 있으니 이를 참고하셔서 구현해 보시면 되겠습니다.

Recommended reading

• Bui Tuong Phong, Illumination for computer generated pictures, Communications of ACM 18 (1975)
• Ray Tracing in One Weekend: https://raytracing.github.io
• lwanger’s python_ray_tracer project: https://github.com/lwanger/python_ray_tracer
• Scratchapixel 3.0 : https://www.scratchapixel.com/index.html