안녕하세요, 2023년도 겨울학기 과학계산 트레이닝 세션의 첫번째 시간에 오신 것을 환영합니다. 뭐든 재미있는 시리즈물이 되기 위해선, 혹은 그런 인상을 주기 위해선 첫 화가 굉장히 중요한데, 첫 주제를 무엇을 할까 한참을 고민하다 그래도 조금 쉽고 재미있을만한 주제를 골라 보았습니다. 이번 주차의 주제는 “The physics behind baseball pitches” 입니다. 이 주제는 실제로 제가 학부 4학년 시절 정말 야구를 좋아했을때 고민해보고 구현해 봤던 문제인데요. 실제로 이번 문제에 쓰인 대부분의 코드는 제가 학부시절 작성했던 코드를 그대로 가져왔습니다. 이 주제는 제가 개인적으로 흥미가 있어 좋아했던 주제이기도 하지만, 이번학기 제가 목표로 하고 있는 “실세계 문제를 간략화해서 프로그래밍으로 구현하여 해결한다”는 목표에 정말 적합한 주제라고 생각합니다. 이건 몇 번을 더 강조해도 부족한 부분인데, 사실 주제 자체는 그렇게 중요하진 않습니다. 어떤 주제라도 주어진 문제를 프로그래밍을 통해 풀어간다는 것에 더 초점이 맞추어 메세지가 전달되기를 바랍니다.
Learning objectives
이번 주차의 목표는 다음과 같습니다.
- 여러분들은 간단한 동역학 시스템에서 주어진 초기 조건에 따라 계의 상태가 어떻게 변화되는지 배우고, 프로그래밍 코드를 통해 이를 구현하게 됩니다.
- 컴퓨터를 이용한 모의 실험(simulation)을 통해 여러분은 계의 상태에 대한 여러 질문들은 답할 수 있게 됩니다.
- 실세계 문제에 존재하는 여러 종류의 물리량을 정량적으로 계산하는 것을 배우게 됩니다.
- 문제와 답을 시각화 하기 위한 여러 기법을 배우고 사용하게 됩니다.
- 야구를 더 좋아하게 됩니다.
Introduction
여러분들은 야구를 좋아하시나요? 야구는 수비 팀의 투수가 던진 공을 공격 팀의 타자가 야구 배트를 이용하여 치고, 경기장의 루(base)를 돌아 점수를 얻는 스포츠 입니다. 따라서 수비 팀의 투수는 최대한 타자가 칠 수 없는 공, 혹은 쳐도 멀리 갈 수 없는 공을 던지려고 노력하고, 공격 팀의 타자는 투수가 던진 공을 받아쳐 수비 팀이 잡을 수 없는 필드 영역에 보내려고 노력합니다. 물론 투수가 아닌 다른 수비 팀의 야수들은 필드 영역에 떨어지는 타자의 공을 잡아 타자를 아웃시키기 위해 노력하구요.
이렇게 축구에 비해 조금 복잡한 규칙을 가지고 있는 야구 이지만, 모든 공격과 수비, 즉 야구의 시작은 투수가 던지는 공에 의해 시작됨을 알 수 있습니다. 이처럼 투수의 중요도는 절대적이며, 단일 경기 내에서 다른 포지션 대비 월등히 높은 영향력을 발휘하게 됩니다. 투수는 타자가 쉽게 칠 수 없는 공을 던지기 위해 공의 속도(velocity)나 움직임(movement)을 바꾸어 강하고, 변칙적인 투구를 하게 됩니다. 물론 아예 칠 수 없는 엉뚱한 곳에 공을 던지는 행위는 투수에게 불리하게 작용되기 때문에, 모든 투수에게는 스트라이크 존이라고 불리는 홈플레이트 근처의 가상의 영역 근처에 정확하게 던지기 위한 높은 제구력(command)이 요구됩니다.
야구의 역사에서 타자들의 타격 기술이 발달한 만큼 투수의 투구도 기술적인 발전을 해 왔습니다. 투수들은 타자가 공을 쉽게 칠 수 없도록 투수가 던질 수 있는 가장 빠른 공인 직구(패스트볼)와, 변칙적인 움직임을 갖는 여러 종류의 변화구(커브, 슬라이더, 체인지업)를 연습하게 됩니다. 하지만 어떻게 투수의 손을 떠난 공이 변칙적인 움직임을 가지고 날아 갈 수 있을까요? 바로 투수들은 손으로 공을 잡는 그립을 바꾸어 공에 특정한 방향의 회전력을 가할 수 있기 때문입니다. 그렇다면 회전하는 공은 왜 변칙적인 움직임을 갖게 되는 걸까요? 이는 유체 속의 회전하며 움직이는 물체에는 운동 방향의 수직으로 마그누스 힘(Magnus force)이 작용하기 때문입니다. 회전하는 물체는 물체 주변에서 유체의 상대적인 속도를 변화시키게 되고 이에 의한 압력 차이가 특정 방향의 양력을 발생시키기 때문이죠. 이처럼 투수가 던지는 변칙적인 공에는 여러 물리학이 숨어 있습니다.
자 이제 여러분이 던진 공 하나에 경기가 이기거나 질 수 있는 상황인 한 점차, 9회말 2아웃 만루 풀카운트 상황을 생각 해 봅시다. 마무리 투수로 올라온 여러분의 손을 떠난 공 딱 하나가 어떻게 날아가는 지에 따라 이 경기는 이기거나, 지게 됩니다. 막중한 부담감 속에서 여러분이 마지막 공을 던지기 위해 와인드업 자세를 취하고 있습니다. 다행이도 여러분은 매우 특별한 능력을 가졌는데요, 바로 여러분은 공의 초기 조건을 정확하게 정의하여 공을 던질 수 있는 능력이 있다는 것입니다. 여러분은 머리속으로 고민을 하고 있습니다. 공을 어떤 속도로 어디에 던질지, 어떤 회전력을 줄지, 어떤 팔 각도와 높이의 릴리즈 포인트에서 공을 놓을지 고민하고 있습니다. 이제 공을 던질 차례입니다. 어떻게 공을 던져야 할지 함께 고민해 봅시다.
아, 그런데 지금 우리 경기장이 없군요? 일단 야구 경기장 부터 같이 만들어 봅시다.
Problem 1: 야구 경기장 만들기
야구장의 전체적인 크기를 결정하는 외야 파울라인의 길이는 야구장에 따라 조금씩 다릅니다. 두산 베어스와 LG 트윈스의 홈구장으로 쓰이고 있는 서울종합운동장 야구장(잠실 야구장)의 경우 홈플레이트에서 중앙 펜스까지의 거리가 125m, 좌우 펜스까지는 120m로 매우 큰 반면, SSG 랜더스가 홈구장으로 사용하고 있는 인천 SSG 랜더스 필드의 경우 중앙 펜스까지 120m, 좌우 펜스까지 95m로 규격이 작아 홈런이 잘 나오는 구장으로 평가받고 있습니다. 하지만 야구장 별로 조금씩 다를 수 있는 외야의 크기와는 달리 투수와 타자가 겨루는 내야의 경우 그 규격이 매우 명확하게 규정되고 있습니다. 지난 120년이 넘는 시간 동안 투수가 공을 던지는 마운드(투수판)로부터 포수가 공을 받는 홈플레이트까지의 거리는 60피트 6인치로(18.44m) 엄격하게 규정되고 있습니다.

특정 야구장을 하나 정해서 외야까지 그대로 재현해 보는 것도 정말 재미있는 일이겠지만, 우리는 투수가 던지는 공에 관심이 있으므로 관심이 되는 시스템을 내야, 그 중에서도 마운드와 홈플레이트 주변으로 한정지어 봅시다.
Problem 1-1: 좌표계를 정의하기
이제 관심이 되는 시스템의 좌표계를 정의해 보도록 하겠습니다. 먼저 x축을 홈플레이트와 마운드를 잇는 가장 긴 축으로 정의하고, y축을 좌우, z축을 높이라고 정의해 보겠습니다. 그렇다면 홈플레이트의 좌표는 x=0, y=0 이 될 것이고, 이에 상대적인 마운드의 중심 좌표는 x=+18.44, y=0 으로 나타낼 수 있습니다. 홈플레이트의 크기는 대략적으로 가로 길이 0.43m , 측면 길이 0.22m, 뒤쪽 삼각형 면의 길이는 0.30m 인 오각형 모양이지만, 편의를 위해 가로, 세로 모두 0.43m의 정사각형이라 가정하겠습니다.
홈플레이트 위에 위치해 있는 가상의 3D 공간인 스트라이크 존의 크기는 현재 타석에 들어선 타자의 무릎과 팔꿈치의 높이에 따라 결정되지만, 우리는 메이저리그의 평균적인 사이즈를 가진 2D 평면으로 스트라이크 존을 단순화 해 보도록 하겠습니다. 우리가 앞으로 사용할 스트라이크 존의 넓이와 높이는 width=0.50m, height=0.55m 이며 홈플레이트로부터 z=+0.52m 떨어져 있다고 가정해 보겠습니다. 시각화의 편의를 위해 스트라이크 존의 깊이를 depth=0.1m로 정의하겠습니다.
반면 투수가 공을 던지는 마운드의 경우 반지름이 약 r=2.75m이며 홈플레이트보다 최소 z=+0.254m 떨어져 있습니다. 옆에서 봤을때 마운드의 높이는 원래 비대칭적이지만, 여기서는 대칭적으로 생겼다고 가정해 보겠습니다. 이제 이 모든 정보를 조합해서 좌표계를 정의하고, 야구 경기장을 만들어 봅시다
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import gridspec
import matplotlib.patches as patches
def drawBaseballField():
fig = plt.figure(figsize=(8,4), dpi=300)
gs = gridspec.GridSpec(2, 2, height_ratios=[1.2, 1],width_ratios=[4.8, 1])
axes = [fig.add_subplot(gs[0,0]),
fig.add_subplot(gs[1,0]),
fig.add_subplot(gs[1,1])]
homeplate_x, homeplate_y = 0.0, 0.0
homeplate_width, homeplate_height = 0.43, 0.43
strikezone_x, strikezone_y, strikezone_z = 0.0, 0.0, 0.52
strikezone_width, strikezone_height = 0.50, 0.55
strikezone_depth = 0.1
mound_x, mound_y, mound_z = 18.44, 0.0, 0.254
mound_radius = 2.75
# Adding home plate
homeplate_patch = patches.Rectangle(xy=(homeplate_x - homeplate_width/2, homeplate_y - homeplate_height/2),
width=homeplate_width, height=homeplate_height,
linewidth=0.5, edgecolor='k', facecolor='none', zorder=20)
axes[0].add_patch(homeplate_patch)
# Adding strike zone
strikezone_ax0_patch = patches.Rectangle(xy=(strikezone_x - strikezone_depth/2, strikezone_y - strikezone_width/2),
width=strikezone_depth, height=strikezone_width,
linewidth=0.5, edgecolor='k', facecolor='none')
axes[0].add_patch(strikezone_ax0_patch)
strikezone_ax1_patch = patches.Rectangle(xy=(strikezone_x - strikezone_depth/2, strikezone_z),
width=strikezone_depth, height=strikezone_height,
linewidth=0.5, edgecolor='k', facecolor='none')
axes[1].add_patch(strikezone_ax1_patch)
strikezone_ax2_patch = patches.Rectangle(xy=(strikezone_x - strikezone_width/2, strikezone_z),
width=strikezone_width, height=strikezone_height,
linewidth=0.5, edgecolor='k', facecolor='none')
axes[2].add_patch(strikezone_ax2_patch)
# Adding pitching mound
mound_circle = patches.Circle((mound_x, mound_y),
radius=mound_radius,
linewidth=0.5, edgecolor='k', facecolor='none')
axes[0].add_patch(mound_circle)
mound_plate = patches.Polygon(xy=[(mound_x-mound_radius, 0),
(mound_x-mound_radius/2, 2*mound_z/3),
(mound_x, mound_z),
(mound_x+mound_radius/2, 2*mound_z/3),
(mound_x+mound_radius, 0)],
linewidth=0.5, edgecolor='k', facecolor='none')
axes[1].add_patch(mound_plate)
mound_plate_ax0 = patches.Rectangle(xy=(mound_x-0.05, -0.3),
width=0.1, height=0.6,
linewidth=0.5, edgecolor='k', facecolor='none', zorder=50)
axes[0].add_patch(mound_plate_ax0)
# Setting lims, ticks, and labels
axes[0].set_ylabel('y (m)')
axes[1].set_xlabel('x (m)')
axes[1].set_ylabel('z (m)')
axes[2].set_xlabel('y (m)')
for a in [0, 1]:
axes[a].set_xlim(-2, +24)
axes[a].yaxis.set_label_coords(-0.07, 0.5)
for a in [1,2]:
axes[a].axhline(0.0, c='k', lw=0.8)
axes[a].set_ylim(-0.1, +2.4)
axes[0].set_ylim(-4.2, +4.2)
axes[0].set_yticks([-4,-2,0,+2,+4])
axes[0].set_xticks([])
axes[1].set_xticks([0, 5, 10, 15, 20])
axes[1].set_yticks([0, 1, 2])
axes[2].set_xlim(-1.2, +1.2)
axes[2].set_yticks([])
axes[2].set_xticks([-1, 0, 1])
plt.subplots_adjust(wspace=0.02, hspace=0.05)
return fig, axes
drawBaseballField()
plt.show()

많은 부분을 간소화 하긴 했지만, 이렇게 좌표계를 정의하고, 정의된 x, y, z 축 에서 홈플레이트, 스트라이크 존, 그리고 마운드를 그려 보았습니다. 어떤가요? 옆에서 보니까 생각보다 마운드의 높이가 굉장히 높죠? 마운드의 높이는 최소 지면으로부터 0.245m 떨어져 있고 일반적으로 마운드의 높이가 높은 경기장일수록 투수에게 유리하다고 알려져 있습니다. 이렇게 함께 좌표계를 정의해 보았지만, 역시 진짜 야구 경기장처럼 보이진 않네요. 한번 시간을 들여 더 비슷하게 꾸며 볼 수 있을까요?
Problem 1-2: 주어진 시스템을 시각화하기 (HW #1)
위에서 정의된 drawBaseballField() 함수를 수정하여 야구장의 여러가지 디테일을 추가해 봅시다. 필드에 잔디도 깔고, 흙도 쌓고, 선도 그리고, 타자가 들어가는 타석도 추가해 봅시다. 결과는 다음과 같습니다.
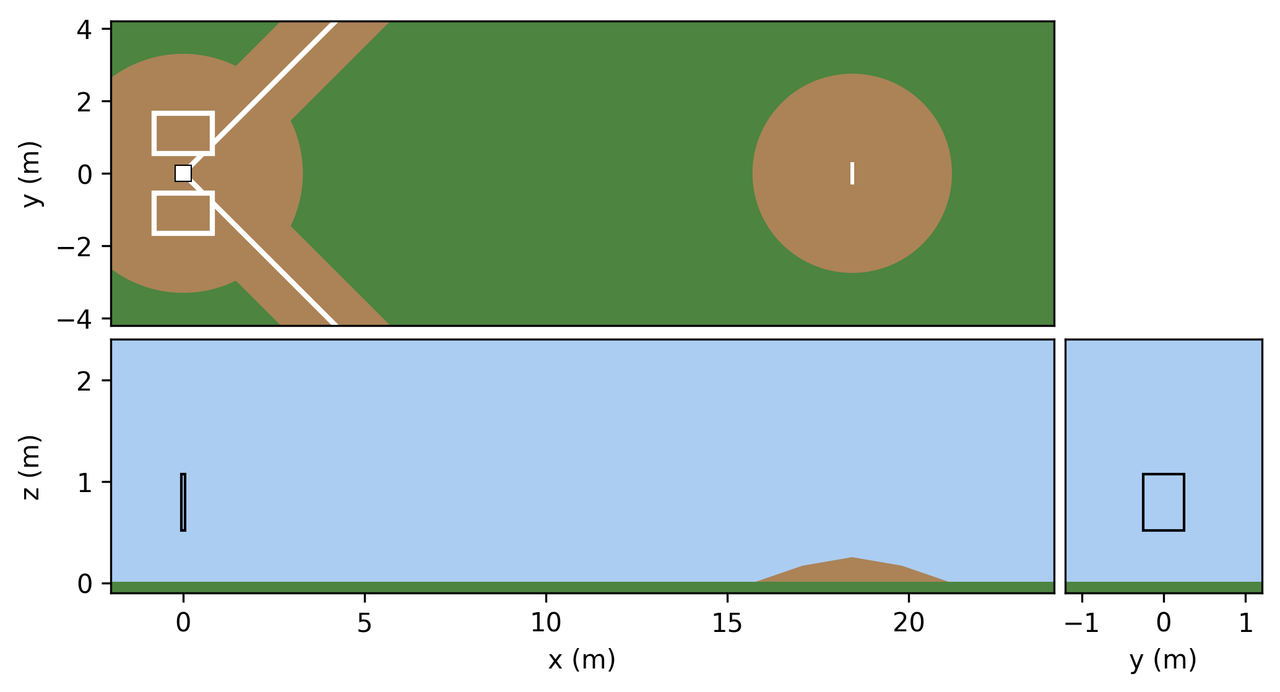
여러분에게 주어지는 첫번째 과제는 바로 drawBaseballField() 함수를 수정하여 위 예시와 최대한 유사하게 주어진 시스템을 시각화 하는 것입니다. 이 과정 속에서 여러분은 그림 속 점, 선, 면 등의 그림 객체들의 순서와 겹침을 고려하여 그림을 그리는 법을 연습하게 됩니다. 따로 의도하거나 정해진 해법은 없으나 이 문제의 의도된 평가 기준은 두가지 입니다. 첫째는 시각화에 있어 필요한 디테일들이 충분한지 검사를 할 것이며, 두번째는 drawBaseballField() 함수의 코드 길이가 120줄이 넘지 않는지 보도록 하겠습니다.
이 문제에서 기준 평점인 A 평점을 받을 수 있는 결과는 120줄 이하의 함수 코드로 위 그림과 같은 수준의 디테일을 담은 경우 입니다. 야구장의 여러 디테일을 더 추가하거나 더 효율적인 코드를 짜신 경우엔 그 이상의 평점을 드리도록 하겠습니다. 화이팅입니다 😃😃😃
Problem 2: 야구공의 동역학 I
드디어 우리에게 멋진 야구장이 생겼습니다. 이제 공을 던질 차례이죠. 위기의 9회말… 을 생각하기 전에 ㅎㅎ 정석적인 우완 투수의 투구폼에 대해 조금 더 생각해 보도록 합시다. 아래 비디오를 통해 KIA 타이거즈 소속의 우완 오버핸드 투수인 장현식 선수의 패스트볼(직구) 투구폼을 볼 수 있습니다. 오버핸드 투수 답게 머리보다 살짝 높은 위치에서 공을 놓는 것을 볼 수 있습니다.

하지만 아무리 오버핸드 투수라고 하더라도 우리의 팔은 양쪽에 달려 있어 공을 y=0 인 x축에 정확하게 맞추어 던지는 것은 불가능 합니다. 우완 투수인 경우 공을 좀 더 왼쪽으로 던지게 되고, 반대로 좌완 투수인 경우엔 공이 왼쪽에서 오른쪽으로 가로지르는 움직임을 보입니다. 이처럼 공의 정확한 초기 조건을 결정하기 위해선 우리가 정의한 좌표계 위에서 투수의 릴리즈 포인트를 알아야 합니다.
Problem 2-1: 투수의 릴리즈 포인트
투구된 야구공의 속도와 궤적을 추적하기 위해 메이저 리그 베이스볼(MLB)에서 사용되는 PITCHf/x 시스템을 통해서 우완 투수의 릴리즈 포인트 데이터를 살펴 보았습니다.

종합적인 여러 데이터에 따르면 수직 릴리즈 포인트 평균은 z=+1.79m, 수직선으로부터 우편향된 릴리즈 포인트의 팔 각도는 오버핸드 투수(왼쪽)의 경우 32.8도인 것을 확인 할 수 있습니다. 투구 할 때의 팔 길이를 약 0.75m로 계산할 경우 우측으로 편향된 수평 릴리즈 포인트는 중심점으로부터 y=+0.63m 떨어져 있다고 가정 할 수 있겠습니다. 또한 투수는 공을 던질때 구속을 높이기 위해 최대한 몸을 앞으로 끌어와 공을 던지게 됩니다. 이를 릴리즈 익스텐션이라 하며 메이저 리그 베이스볼의 평균적인 익스텐션 길이는 약 x=-1.98m입니다.
이제 우완 오버핸드 투수가 위에서 정의한 릴리즈 포인트에서 스트라이크 존 한 가운데에 공을 패스트볼 구속 150km/h로 직선으로 던진 상황을 가정해 보겠습니다. 먼저 야구공을 추상화한 객체를 만들어야 하는데요, 객체지향 프로그래밍이 익숙하지 않다면, 이 기회에 연습해 봅시다.
class Baseball():
def __init__(self,
velocity,
target,
x_release = -1.97,
y_release = 0.63,
z_release = 1.79):
self.target = np.array(target)
self.release_point = np.array([18.44+x_release, y_release, z_release])
self.direction = self.target - self.release_point
self.velocity = 0.277* velocity * self.direction / np.linalg.norm(self.direction)
def get_trace(self, dt = 0.01):
self.dt = dt
position = np.copy(self.release_point)
trace = [position]
while True:
position += self.dt * self.velocity
trace.append(np.copy(position))
if position[0] <= -1.0:
break
self.trace = np.array(trace)
def draw_trace(self, axes):
for a, idx in enumerate([[0,1], [0,2], [1,2]]):
axes[a].scatter(self.release_point[idx[0]], self.release_point[idx[1]], s=30, c='w',
linewidths=1, marker='x', zorder=100)
axes[a].scatter(self.trace[:,idx[0]], self.trace[:,idx[1]],
alpha=np.linspace(0.1, 1, len(self.trace)), s=2, facecolor='w', zorder=100)
strikezone_z = 0.52
strikezone_height = 0.55
target_height = strikezone_z + strikezone_height/2
ball = Baseball(velocity=150, target=(0, 0, target_height))
fig, axes = drawBaseballField()
ball.get_trace()
ball.draw_trace(axes)
plt.show()

공에 어떠한 외력도 작용하지 않고 초기 속도에 의한 등속 운동을 가정한 상황에서 투구된 야구공의 궤적을 그려보면 다음과 같습니다. 공이 직선으로 정확하게 스트라이크 존의 가운데를 통과하는 것을 볼 수 있습니다. 하지만 실제로 투수가 던진 야구공에는 여러 종류의 힘이 작용하는데요, 일단… 야구장이 지구에 있다는 가정 하에, 첫번째로 고려해야 하는 것은 중력입니다. 야구공은 중력에 의해서 -z 방향으로 자유낙하 하기 때문에 실제 스트라이크 존의 가운데를 향해 던진다고 하더라도 점점 아래로 휘어지게 됩니다. 이제 중력을 고려하여 시뮬레이션 해 보겠습니다.
Problem 2-2: 야구공에 작용하는 중력
중력에 의한 자유낙하는 중력가속도 g=9.8m/s^2에 질량을 곱한 값으로 계산 할 수 있습니다. 중력에 의한 자유낙하의 경우 아래쪽으로 힘을 받기 때문에 방향은 -z가 됩니다.
\[\vec{F_{g}} = -mg \hat{z}\]
이 힘을 야구공의 질량으로 나누어 주면 가속도를 계산 할 수 있는데요, 물론 이 경우엔 중력을 제외한 다른 외력이 존재하지 않기 때문에 당연히 가속도는 -g가 될 것입니다. 이 가속도는 매 초마다 공의 속도에 더해져 공의 위치를 변화시키게 됩니다.
class Baseball():
def __init__(self,
velocity,
target,
x_release = -1.97,
y_release = 0.63,
z_release = 1.79):
self.g = 9.8 # acceleration due to gravity in m/s^2
self.mass = 0.148 # baseball mass in kg
self.target = np.array(target)
self.release_point = np.array([18.44+x_release, y_release, z_release])
self.direction = self.target - self.release_point
self.velocity = 0.277* velocity * self.direction / np.linalg.norm(self.direction)
self.a = np.zeros(3)
def get_force(self):
F_g = np.array([0,0,-self.mass*self.g])
F_total = F_g
self.a = F_total/self.mass
def get_trace(self, dt = 0.01):
self.dt = dt
position = np.copy(self.release_point)
trace = [position]
while True:
self.velocity += self.dt * self.a
position += self.dt * self.velocity
trace.append(np.copy(position))
if position[0] <= -1.0 or position[2] <= 0:
break
self.trace = np.array(trace)
def draw_trace(self, axes, c='w'):
for a, idx in enumerate([[0,1], [0,2], [1,2]]):
axes[a].scatter(self.release_point[idx[0]], self.release_point[idx[1]], s=30, c=c,
linewidths=1, marker='x', zorder=100)
axes[a].scatter(self.trace[:,idx[0]], self.trace[:,idx[1]],
alpha=np.linspace(0.1, 1, len(self.trace)), s=2, facecolor=c, zorder=100)
strikezone_z = 0.52
strikezone_height = 0.55
target_height = strikezone_z + strikezone_height/2
ball = Baseball(velocity=150, target=(0, 0, target_height))
fig, axes = drawBaseballField()
ball.get_trace()
ball.draw_trace(axes, c='k')
ball.get_force()
ball.get_trace()
ball.draw_trace(axes, c='w')
plt.show()
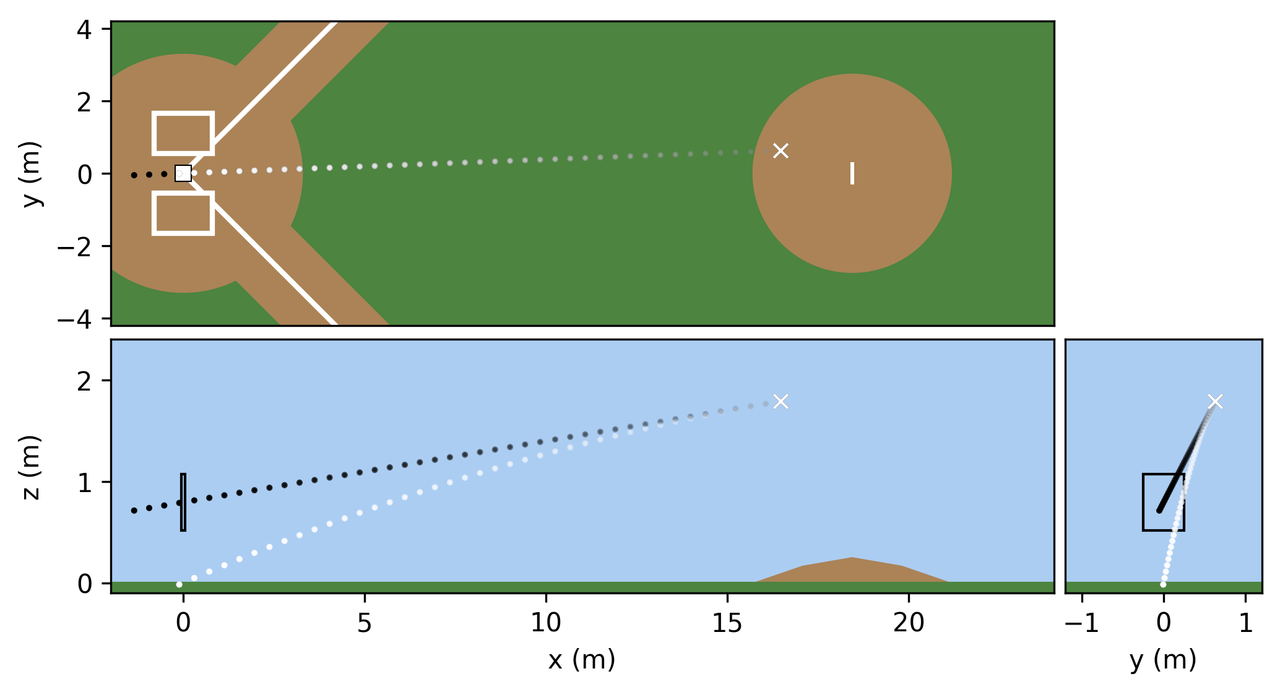
중력이 고려되지 않은 경우의 투구(검은색 궤적)과 중력이 존재할 때의 투구(흰색 궤적)을 그려 보았습니다. 중력은 -z 방향으로만 영향을 미치는 힘이기에, x축과 y축 상에서의 차이는 관찰되지 않는 모습입니다. 코드에서 볼 수 있다 시피 이제 여러분은 get_force() 메서드를 통해 공에 작용하는 여러 힘을 고려해 볼 수 있습니다. 지금은 이제 중력만 고려해 보았구요. 공이 스트라이크 존을 벗어나 땅으로 들어가려 하고 있으니, 목표로 하는 target 좌표를 수정해야 할듯 합니다. 중력이 없을 때 (0m, 0m, +1.5m) 좌표에 도달할 것이라 가정을 하고 공을 던지도록 하겠습니다. 이 궤적은 공에 회전력을 주지 않은 상태로 던진 후 중력에 의해 자유낙하하는 공의 궤적이 됩니다.

여기서 깜짝 퀴즈가 있습니다. 위 __init__() 메서드에 있는 다음 코드에서 계수 0.277이 의미하는 바가 무엇일까요? 중간 중간 드리는 깜짝 퀴즈는 모두 평점에 반영됩니다.
self.velocity = 0.277 * velocity * self.direction / np.linalg.norm(self.direction)
Problem 3: 야구공의 동역학 II
와 축하합니다! 드디어 우리에게 움직이는 야구공이 생겼습니다. 여기까지 잘 따라오셨나요? 이제 우리는 중력과 더불어 야구공에 적용되는 또 다른 두개의 외력인 항력(drag force)과 마그누스 힘(magnus force)을 배우고, 이를 구현해 볼 것입니다. 힘의 방향이 항상 -z로 같은 중력과 달리 항력과 마그누스 힘은 공의 현재 진행 방향에 따라 힘의 방향이 달라집니다. 공에 백스핀이 걸린 상황에서 포물선 운동을 하고 있는 경우를 고려해 보겠습니다.

위 그림에서 알 수 있듯, 공의 현재 진행 방향과 무관하게 아래쪽( -z)을 향하는 중력과 다르게 항력(drag)의 경우 언제나 공의 진행 방향과 반대 방향의 힘을 받는 것을 볼 수 있고, 마그누스 힘(그림에서 Lift로 표시됨)은 공의 진행 방향에 대해 수직인 것을 볼 수 있습니다. 주의하실 점은 마그누스 힘은 언제나 공의 진행 방향에 수직이지만, 공에 걸린 스핀의 방향에 따라 수직인 평면 내에서 힘의 방향이 결정됩니다. 그림과 같이 백스핀인 경우에는 공이 떠오르는 방향으로 힘이 작용하며 반대로 탑스핀인 경우 공이 가라앉는 힘이 작용 합니다. 두 외력 중, 먼저 항력을 고려해 보겠습니다.
Problem 3-1: 유체 내에서의 저항력 (HW #2)
야구공이 유체(대부분의 야구장에서 이는 공기 입니다…)를 지나는 경우 공의 진행방향의 반대로 저항력이 발생합니다. 이를 항력(drag force)라 하며 매 순간 공의 진행 방향에 대해 반대로 작용합니다. 야구공에 작용하는 항력의 크기와 방향은 다음과 같습니다.
\[\vec{F_{d}} = -\frac{1}{2}C_{D}\rho A v^{2} \frac{\vec{v}}{v}\]
항력은 공의 속도의 제곱에 비례하며 속도의 반대 방향인 것을 알 수 있습니다. 계산에 필요한 항력계수($C_{D}$)와 공기의 밀도($\rho$), 야구공의 단면적($A$)은 메이저리그 베이스볼의 투구 추적 시스템인 PITCHf/x 를 통해 얻은 데이터에서 찾아 볼 수 있으며 각각 다음과 같습니다.
- $C_{D}=0.40$
- $\rho=1.225 \text{ kg}/\text{m}^{3}$
- $A=0.00426 \text{ m}^{2}$
이제 여러분은 Baseball 클래스의 get_force() 메서드를 수정하여 야구공에 걸리는 항력을 계산하시면 됩니다.
def get_force(self):
F_g = np.array([0,0,-self.mass*self.g])
F_d = #???
F_total = F_g + F_d
self.a = F_total/self.mass
답은 get_force() 메서드가 공의 현재 진행 방향을 입력으로 받아 실시간으로 작용하는 항력의 방향과 크기를 계산하는 내용이 포함되어야 합니다. 힘은 스칼라 값이 아닌 3차원 벡터로 계산되어야 한다는 점을 꼭 잊지 않으시길 바랍니다. 화이팅입니다!
Problem 3-2: 스핀의 방향과 마그누스 힘 (HW #3)
야구공의 진행 방향을 고려하지 않아도 되는 중력, 야구공의 진행 방향만 고려하면 되는 항력과 다르게 마그누스 힘은 야구공의 진행 방향과 야구공의 스핀의 방향까지 함께 고려해야 합니다. 야구공이 회전하게 되면 주변 유체와 함께 회전하는 쪽과, 주변 유체의 상대적인 진행 방향과 반대로 회전하는 쪽이 생겨 압력 차가 발생하기 때문입니다. 야구공에 작용하는 마그누스 힘의 크기와 방향은 다음과 같습니다.
\[\vec{F_{m}} = \frac{1}{2}C_{L}\rho A v^{2} ({\hat{w}}\times \hat{v})\]
계산에 필요한 양력계수(Lift coefficient, $C_{L}$)는 일반적으로 야구공의 회전 속도에 따라 증가합니다. 패스트볼, 슬라이더, 체인지업 등 투수의 구종에 따라 야구공의 회전 속도가 조금씩 다르므로 정밀하게 계산하기 위해선 구종 별 양력계수를 계산해야 하지만 평균적으로 $C_{L}=0.22$ 정도를 갖는다고 유효 범위 내에서 근사 할 수 있습니다. 나머지 계수는 항력의 식에서 사용된 값과 같고, 이제 마그누스 힘의 방향을 결정하는 벡터곱(vector product, ${\hat{w}}\times \hat{v}$) 항을 보겠습니다. 이를 이해하기 위해서 여러분들은 두가지 개념에 대한 선행 지식이 필요합니다.

-
회전 방향을 벡터(${\hat{w}}$)로 표현하기
이는 비단 야구공에만 적용되는 개념은 아니다 보니 이미 고등학교나 대학교 물리 시간에 배우셨을 수도 있지만, 스핀에 대한 벡터는 반시계 방향의 회전축의 방향을 따릅니다. 아래 두 경우를 고려해 봅시다. 공의 진행 방향이 화면을 뚫고 나를 향하고 있다고 생각해 봤을때(이 말이 이상하게 들릴지 모르겠지만, 이는 매우 흔히 사용되는 표현입니다) 탑스핀과 백스핀의 방향은 아래 그림과 같습니다. 그리고 두 스핀 벡터의 방향은 우리가 정의한 좌표계에서 탑스핀은 -y, 백스핀은 +y에 해당하게 됩니다.
-
야구공의 회전 방향 벡터와 속도 백터의 벡터곱을 계산하기
이제 정의된 야구공의 회전 방향 벡터(스핀 벡터, $\vec{\omega}$)와 속도 벡터($\vec{v}$)의 벡터곱 연산을 통해 마그누스 힘 벡터의 방향을 계산 할 수 있습니다. 이때 두 벡터곱 연산의 값은 마그누스 힘 벡터의 방향을 결정할 뿐, 마그누스 힘 벡터의 크기와 무관하다는 점을 수식을 통해 알 수 있습니다.
두 개념을 이해하셨다면 이제 Baseball 클래스의 get_force() 메서드를 수정해 마그누스 힘을 구현하시면 됩니다. 아래 코드에서 항력인 $F_{d}$와 마그누스 힘인 $F_{m}$에 해당하는 코드를 작성해 봅시다. 따로 정해진 방법은 없고, 코드가 효율적으로 동작하는 선에서 자유롭게 작성하시면 되겠습니다. 두 외력을 정확하게 구현하신 경우 기준 평점을 드리도록 하겠습니다.
def get_force(self):
F_g = np.array([0,0,-self.mass*self.g])
F_d = #???
F_m = #???
F_total = F_g + F_d + F_m
self.a = F_total/self.mass
자 이제 여러분은 공을 던질 모든 준비를 마쳤습니다. 이제 던지고자 하는 구종에 맞춰 공에 스핀만 주면 되는데요, 아래에 5 종류의 투구 예시를 준비하였고, 이중 여러분은 패스트볼, 커브, 슬라이더의 투구 데이터를 이용하여 각 구종을 시뮬레이션 하고, 결과를 시각화 해오시면 됩니다. 여러분이 이 섹션까지 야구공에 작용하는 세 외력인 중력, 항력, 마그누스 힘을 정확하게 구현 하셨다면 투구의 종류(구종)와 무관하게 입력한 초기조건 데이터에 따라 정확한 결과가 나올 것이니 앞으로는 크게 어려운 것이 없을 것입니다.
Problem 3-3: 패스트볼 (HW #4)
변화구 대비 빠른 구속을 가져 타자의 타이밍을 뺏기에 유리한 패스트볼은 가장 널리 쓰이는 투수의 무기이자 위력적인 구종입니다. 투수들은 대부분의 상황(60~70%)에서 패스트볼을 투구하며, 스트라이크 존 코너를 공략 할 수 있는 뛰어난 제구력을 가진 마무리 투수의 경우 거의 패스트볼만 투구하는 경우도 있습니다. 패스트볼은 한국에서 흔히 직구라고도 불리며 변화구 대비 수직 및 수평 움직임(movement)이 적은 것이 특징입니다. 이 움직임이 적어 보이는 이유엔 바로 패스트볼 특유의 백스핀이 있기 때문입니다. 실제 패스트볼의 스핀을 봐 볼까요? 왼쪽은 피칭머신을 이용해 던진 패스트볼이며, 오른쪽은 실제 우완 투수가 던지는 패스트볼의 스핀입니다.

투구된 패스트볼은 공 아래쪽의 경우 공의 진행 방향과 일치된 스핀을 갖고, 공 위쪽의 경우 공의 진행 방향과 반대의 스핀을 갖습니다. 이를 백스핀이라고 부르며 공은 위, 아래의 압력 차에 의해서 떠오르게 됩니다. 물론 공에는 마그누스 힘 대비 상대적으로 큰 중력이 항상 작용하기 때문에, 실제로 공이 “떠오르는” 현상은 관찰 할 수 없습니다. 상대적으로 덜 떨어지게 되는 것이지요. 이제 패스트볼을 시뮬레이션 해 봅시다. 극단적으로 백스핀 컴포넌트만 있다고 가정을 하게 되면 스핀 벡터의 방향은 우리가 정의한 좌표계에서 +y 방향에 해당하게 됩니다.
패스트볼의 예시로 우완 투수인 삼성 라이온즈 오승환 선수의 94마일(151.2km/h) 하이패스트볼을 예시로 가져와 보았습니다. 하이패스트볼은 이처럼 극단적으로 적은 수직 무브먼트와 빠른 구속으로 타자의 타이밍을 뺏거나 타구의 발사각을 낮추는 효과를 가져 최근 널리 쓰이고 있습니다.

오승환 선수의 데이터를 이용한 시뮬레이션 결과는 다음과 같습니다.
ball = Baseball(velocity=151.2, target=(0, -0.1, 1.4), spin=(0,1,0))
fig, axes = drawBaseballField()
ball.get_trace()
ball.draw_trace(axes)
plt.show()

어떤가요? 오승환 선수의 실제 패스트볼 궤적과 굉장히 유사하죠? 수직 무브먼트가 적고, 타자의 눈높이에서 빠르게 타이밍을 뺏는 하이패스트볼의 특징을 볼 수 있습니다.
Problem 3-4: 사이드암 투수의 패스트볼
이렇게 공의 움직임이 크게 억제된 패스트볼 이지만, 오버핸드 투수 대비 릴리즈 포인트가 낮고, 패스트볼 스핀에 횡이동 요소가 있는 사이드암 투수의 경우 매우 흥미로운 패스트볼 움직임을 보입니다. 다음은 우리나라 프로야구의 전설적인 사이드암 투수였던 삼성 라이온즈, KIA 타이거즈 소속 임창용 선수의 전매특허인 구속 153km/h “뱀직구”의 궤적입니다. 왼쪽으로 진행하던 공이 좌타자 몸쪽으로 강하게 테일링이 걸려 휘어져 들어가는 것을 볼 수 있습니다.

임창용 선수의 신체 조건과 릴리즈 포인트, 강한 -z축 성분을 갖는 스핀 정보를 입력하면 우측으로 휘는 뱀직구를 재현 할 수 있습니다.
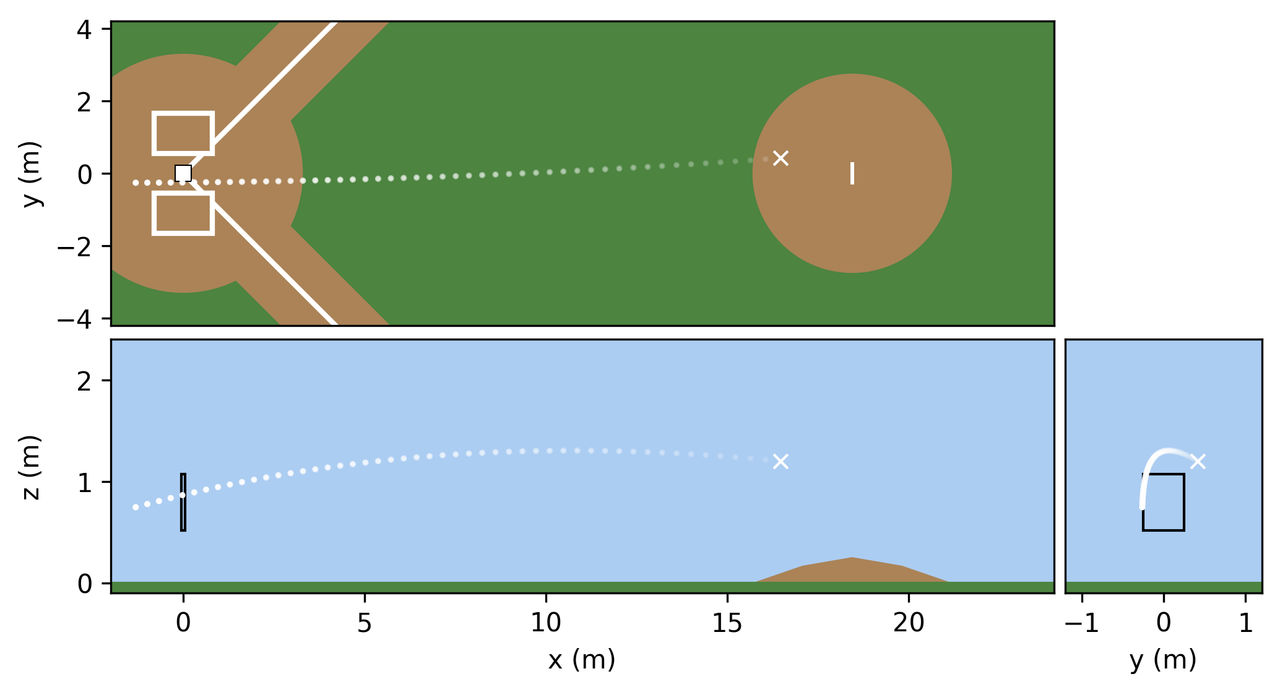
Problem 3-5: 커브 (HW #5)
백스핀을 가진 패스트볼과 반대로 커브 혹은 커브볼은 완전한 탑스핀을 갖도록 투구합니다. 물론 피칭머신이 아닌 이상 완벽하게 탑스핀 요소만 넣는 것은 불가능합니다만, 그래도 스핀 방향의 대부분이 -y 방향을 향하게 됩니다.

탑스핀에 의해 발생된 마그누스 힘의 방향은 아래쪽을(-z) 향하게 되며 따라서 중력에 의한 효과보다 “더 떨어지는” 현상을 보이게 됩니다. 멋지게 수직으로 떨어지는 커브볼은 시계의 12시 방향에서 6시 방향으로 떨어진다고 하여 12-6 커브라고 부르기도 합니다. 현재는 은퇴했지만 한때 한국 프로야구 최고의 커브볼러중 한 명이었던 KIA 타이거즈 김진우 선수의 131km/h 폭포수 커브 궤적을 보도록 하겠습니다.

김진우 선수의 투구 데이터를 이용하여 커브볼을 시뮬레이션 해 보도록 하겠습니다.
ball = Baseball(velocity=131, target=(0, -0.05, 2.0), spin=(0,-1,0))
fig, axes = drawBaseballField()
ball.get_trace()
ball.draw_trace(axes)
plt.show()

여러분이 Baseball 클래스를 잘 구성했다면 이제 바꿀 것이 별로 없습니다. 이제부터는 공의 초기 조건만 입력하면 여러 변화구를 시뮬레이션 할 수 있기 때문입니다. 스핀의 방향이 -y인 것을 주목해 주시기 바랍니다. 여기서 깜짝 퀴즈가 있습니다. 우리가 시뮬레이션 한 오승환 선수의 패스트볼과 김진우 선수의 커브볼은 릴리즈 포인트에서 홈플레이트(x=0)까지 날아가는데 걸리는 시간이 몇 초 차이가 날까요?
Problem 3-6: 슬라이더 (HW #6)
다음은 변화구의 대표주자, 슬라이더 입니다. 슬라이더는 대부분의 투수가 가장 먼저 익히는 변화구이자, 던지는 손의 반대 방향으로 휘어 나간다는 특성 때문에 같은 손 타자를 상대하는데 유리한 것으로 잘 알려져 있습니다. 타자들은 몸 바깥쪽으로 휘어나가는 공에 특히 약한데, 우완 투수가 우타자를 상대하는 경우엔 슬라이더가 그런 특징을 보입니다. 우완 투수가 던지는 슬라이더는 좌측으로 휘어 나가기 때문이죠!
역시 커브 볼과 마찬가지로 실제 투수는 피칭머신이 아니다 보니 이상적인 슬라이더의 스핀 방향인 +z 방향으로 던질 수 없지만 우완 투수는 검지와 중지를 이용해 공의 오른쪽을 강하게 밀어 야구 공에 +z 방향의 회전력을 가합니다.

쓰리 쿼터 정도의 높이에서 공을 투구하는 맥스 슈어저 선수의 구속 138.4km/h 의 슬라이더를 보시겠습니다. 우타자 바깥쪽으로 흘러가나는 움직임이 인상적입니다.

맥스 슈어저 선수의 투구 데이터를 입력하여 슬라이더를 구현해 보도록 하겠습니다. target coordinate의 y좌표가 투수의 오른쪽인 y=+0.4m임에도 불구하고 스핀에 의해 반대 방향인 좌측(-y)으로 흘러가는 모습을 볼 수 있습니다. 쓰리 쿼터 높이에서 투구하기 때문에 릴리즈 포인트를 일부 수정하였습니다.
ball = Baseball(velocity=138.4, target=(0, +0.4, 1.4), spin=(0,0,1), y_release=0.75, z_release=1.4)
fig, axes = drawBaseballField()
ball.get_trace()
ball.draw_trace(axes)
plt.show()

Problem 3-7: 체인지업
그렇다면 투수가 반대 손 타자를 상대할때 효과적이라고 알려진 변화구는 무엇일까요? 이는 마지막으로 소개할 변화구는 체인지업 입니다. 현대 야구에서 그 활용도에 대한 주목이 점점 높아지고 있는 체인지업은 우완 투수가 던질 경우 좌타자의 헛스윙을 유도할 수 있습니다. 제가 생각하기에 국내 투수들 중 가장 인상깊은 체인지업 무브먼트를 보이는 KIA 타이거즈 우완 언더핸드 투수인 임기영 선수의 체인지업을 보도록 하겠습니다.

좌타자 방망이 끝이 닿지 않는 곳으로 공이 휘어저 나가며 헛스윙을 유도하는 모습이 인상적입니다. 임기영 선수의 투구 데이터를 입력하여 체인지업을 시뮬레이션 해 보도록 하겠습니다. 언더핸드 투수이므로 낮은 수직 릴리즈 포인트를 갖습니다.
ball = Baseball(velocity=122, target=(0, -0.3, 1.7), spin=(0,0,-1),y_release = 0.4, z_release = 0.8)
fig, axes = drawBaseballField()
ball.get_trace()
ball.draw_trace(axes)
plt.show()

Problem 4: 투구 분포도 시각화 (HW #7)
여러분! 여기까지 잘 따라오셨나요? 정말 고생하셨습니다. 이제 남은 마지막 숙제는 지금까지 잘 따라 오셨다면 무척 쉬울 것이라 생각 됩니다. 지금부터 해 볼 것은 몬테 카를로 시뮬레이션을 이용하여 투수의 릴리즈 포인트에 따른 투구 분포 확률을 계산해 보고, 이를 시각화 해 보겠습니다.
실험 조건은 다음과 같습니다. 베이스가 되는 투구 데이터는 위에서 시뮬레이션한 맥스 슈어저 선수의 슬라이더를 사용합니다. 다만 실제 투구의 변칙성과 불규칙성을 반영하기 위해서 투수의 릴리즈 포인트, 타겟 위치, 구속 등을 정규분포로부터 샘플링 합니다. 예를 들어 x_release의 경우 평균이 -1.9이고 표준편차가 0.2인 정규분포를 따릅니다.
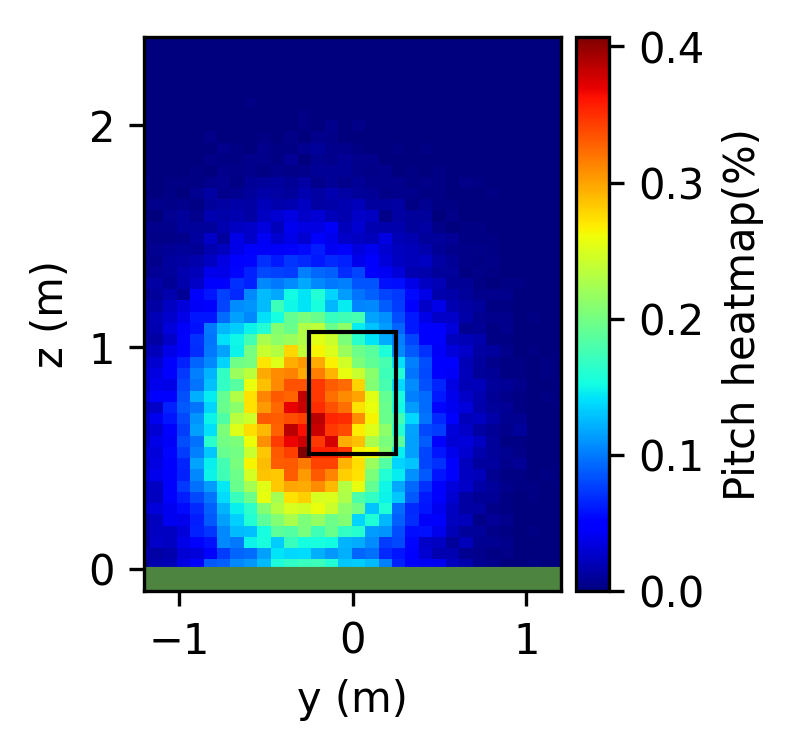
이번 문제는 몬테 카를로 시뮬레이션과 아래 정규분포를 따르는 투구 데이터를 이용하여 총 10만번의 투구 궤적을 계산하고 각 궤적이 스트라이크 존을 지날 때의 투구 분포도(heatmap)를 그리시면 됩니다. 기준 평점을 받기 위한 조건은 두가지 입니다. 첫째는 아래 그림과 유사한 투구 분포도를 시각화 하셔야 합니다. 정해진 방법은 없으니 자유롭게 방법을 찾아보시면 되겠습니다. 두번째는 시뮬레이션 시작부터 그림을 그려 출력하는 전체 시간이 10분이 넘으면 안됩니다. 컴퓨터에 따라 실행 속도가 다르겠지만, 제 노트북에서 여러분의 코드를 테스트 해 볼 것이며, 제 코드의 경우 제 컴퓨터에서 5분 12초가 소요되었습니다. 제 생각에 시뮬레이션 시간은 거의 차이가 날 것 같지 않으니, 시각화 코드를 효율적으로 짜는데 노력을 들이시면 좋을것 같습니다.
N = 100000
x_release = np.random.normal(-1.9, 0.2, N)
y_release = np.random.normal(0.6, 0.1, N)
z_release = np.random.normal(1.4, 0.2, N)
y_target = np.random.normal(0.3, 0.4, N)
z_target = np.random.normal(1.8, 0.4, N)
velocity = np.random.normal(138, 5, N)
마치며
드디어 길었던 첫 주차 과학계산 트레이닝 세션이 끝났습니다. ㅎㅎ 여러분들이 어떻게 생각 하실지 모르겠지만, 여기까지 잘 따라오셨다면 아마 이미 많은 고민을 하셨고, 그 고민 속에서 어느정도의 성장을 하셨을 것이라 생각 합니다. 우리가 비록 실제 야구에서 일어나는 더 복잡한 동역학을 재현해 본 것은 아니지만, 그래도 여러분들은 이 과제를 수행하며 시스템의 정의, 시뮬레이션, 데이터 시각화, 코드 최적화 등을 연습하셨습니다. 저에겐 제가 정말 좋아하는 주제이고, 학부 시절 굉장히 재밌게 접근했던 문제로 기억하고 있지만, 사실 야구라는 주제가 몇몇 분들에겐 다소 재미 없는 이야기로 들리셨을수도 있겠습니다. 하지만 다시 한번 강조하고 싶은 점이 있다면, 어떤 주제인가는 크게 중요하지 않은것 같습니다. 여러분들이 “어떤” 실세계 문제를 컴퓨터를 이용하여 실제로 풀었다는 경험이 훨씬 중요하고, 제가 전달하고 싶은 메세지 입니다. ㅎㅎ 그래도 다음 세션은 더 재미있는 문제가 될지도 몰라요…
숙제 제출은 총 2주의 시간을 드릴 예정 입니다. 얼마나 많은 분들이 제출해 주실까 걱정이 되지만… 단 한분이라도 끝까지 이번 주차의 학습을 마치시는 분이 계시다면, 다음 주차는 더 재미있고 도움이 될 수 있는 주제로 준비해 보겠습니다. 끝까지 정말 고생하셨습니다. 감사합니다.
Recommended reading